Reaction-Rate Theory - Fifty Years after Kramers 翻译（一）

​ 阅读化学动力学经典文献：Reaction-Rate Theory: Fifty Years after Kramers (Hänggi, Talkner & Borkovec, 1990) 顺便翻译了摘要和介绍部分。后续阅读所得将会呈现在此文(Chemical Dynamics. I. A Historical Introdcution)中。

Abstract

速率系数的计算是非线性科学的一个重要分支，在物理学、化学、工程学和生物学中都有重要的应用。在Kramers关于热激活势垒穿越的开创性论文发表50年后，作者报告、扩展和解释了我们目前对噪声激活逃逸理论的许多理解，其中许多值得注意的贡献来自物理学和物理化学界。讨论了气体和凝聚相中单维和多维亚稳态系统(包括场)的理论和数值方法。比较了多维过渡态理论和中强摩擦下的Kramers反应速率理论的作用；作者强调了物理场景以及单分子速率理论与弱阻尼系统下的Kramers理论的密切联系。介绍了考虑记忆摩擦的速率理论，以及一个涵盖了弱-中-强摩擦整个区间的统一理论框架(周转理论, turnover theory)。通过平均第一通过时间技术，阐明了在各种物理上不同的亚稳势构型中噪声激活逃逸的特性。此外，还确定了可能具有多个亚稳非平衡态的驱动系统中逃逸的作用和复杂性。在较低温度下，量子隧穿效应开始主导速率机制。讨论了Kramers理论的早期量子方法和最新的量子版本，从而提供了在所有温度下耗散逃逸事件的描述。此外，还试图讨论与Kramers反应速率理论有关的突出的实验工作，并指出在理论上和未来研究中最重要的领域。

Introduction

​ 亚稳态逃逸问题在几乎所有的科学领域都是普遍存在的。反应速率理论在化学动力学、固体中的相平衡理论、均相成核和电输运理论等领域都有重要的贡献。人们很早就认识到速率过程具有稀有事件的特征，也就是说，与表征局部稳定状态的动态时间尺度相比，速率过程是发生在长时间尺度上的现象（见 Fig. 1）。

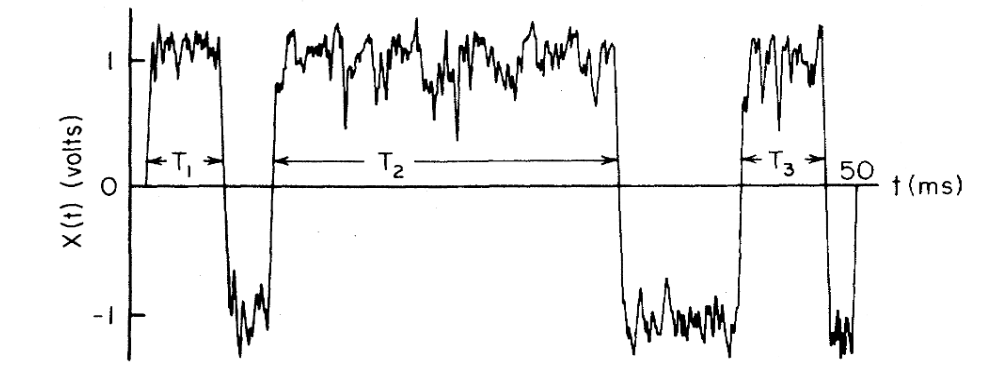
FIG. 1. 一个在对称双稳势\(U(x)=-\frac{1}{2}x^2+\frac{1}{4}x^4\)中对随机逗留时间{T₁,T₂,etc.}的典型随机实现采样，亚稳态位于\(x=\pm1\)处。数据来自于Hänggi Mroczkowski, Moss, and McClintock, (1985)

当Svante Arrhenius对各种反应速率数据进行广泛的讨论，指出反应速率的对数是反转温度(inverse temperature)\(\beta=(k_BT)^{-1}\)的函数，速率理论这门学科诞生了。换句话说，速率系数k，或简单地说逃逸速率(rate of escape)，遵循Van't Hoff-Arrhenius定律(Van't Hoff, 1884, Arrhenius, 1889)^{<span class="hint--top hint--rounded" aria-label="Logan (1982)、Laidler (1984, 1987)和Stiller (1989)给出了Arrhenius方程发展的美妙历史评论。审视Arrhenius的原文使得评论的作者们感到尴尬，他们认识到Arrhenius并未画出一条Arrhenius曲线，此外Arrhenius还将通常所谓的Arrhenius方程 \(k=\nu exp-(B/T)\) 归功于Van't Hoff。然而，在他对速率数据的讨论中，他引入了一个"假想体"，即通常被称为"活化复合物"的活性状态，并提出了正常和活性反应物分子之间的平衡。这一概念本身无疑是对反应速度理论最重要的贡献。">[1]} \[ k=\nu exp(-\beta E_b),\tag{1.1} \] 式中：\(E_b\)为活化所需的阈值能量，\(\nu\)为指前因子。Fig 2描绘了在较大温度范围内各种反应的Van't Hoff-Arrhenius图。在19世纪后期，该论题定量上的进展缓慢。人们意识到只有通过噪声辅助的跳跃事件才能逃离局域稳态。因此，逃逸速率的计算乍看之下是一个令人望而却步的问题。该领域不得不等待一个关于波动(fluctuations)的理论。这种对波动的关注始于Lord Rayleigh (1891)、Einstein (1905)、Smoluchowski (1906, 1913, 1915)、Fokker (1913, 1914)、Planck(1917)、Ornstein (1917), Pontryagin等(1933), 以及其他许多人的开拓性贡献。Chandrasekhar(1943)的一篇优秀论文综述了早期关于布朗运动理论的工作。关于布朗运动早期研究的更详细的介绍可以参见Pais (1982)和Coffey (1985)最近的综述文章。当然，速率理论的第一项重要工作必须归功于Smoluchowski(Smoluchowski, 1917)。他导出了扩散控制的胶体聚沉速率系数 k_c，\(k_c=4\pi(D_A+D_B)(R_A+R_B)\)，其中\(D_{A,B}\)是和\(R_{A,B}\)分别是净化剂物种A、B的扩散系数和半径。扩散控制的相遇反应这一重要领域的现状最近得到了Calef和Deutch ( 1983 )的精彩审视。

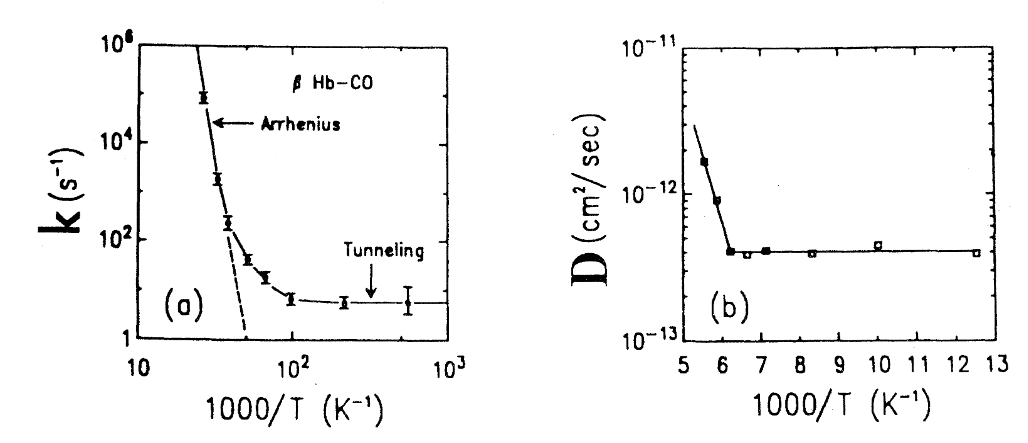
FIG. 2. 两种不同的物理体系的反应速率数据的Van't Hoff-Arrhenius图中都出现了热激活和隧穿事件：(a) CO迁移到血红蛋白(Alberding et al., 1976; Frauenfelder, 1979)一条单独的β链上的速率；( b )相对H覆盖度为0.1时原子氢在钨( 110 )面上运动的扩散系数D。(数据来源于DiFoggio和Gomer, 1982)。扩散系数D与跳跃速率k成正比。

​ 与一般活化速率理论相关的第一个定量思想起源于对过饱和蒸汽((Frenkel, 1955 ; Zinsmeister , 1970 ; Abraham , 1974)中均相成核的研究。自然地，均相成核是一个相当复杂的课题，目前还没有完整的解决方案，即各种有趣的基本问题仍然没有解决(Abraham, 1974; Binder and StauAer, 1976; Langer, 1980; Gunton San Miguel, and Sahni, 1983)。在一篇开创性论文中，Farkas (1927) 通过处理到达液滴或从液滴中蒸发的原子的详细动力学来考虑均相成核的速率。他引入了一种今天被称为"Markovian生灭过程"的方法^[2]。此外，在他的论文中，Farkas 描述了任何速率计算背后的基石思想——显然，从亚稳态逃逸的速率表征为穿过将产物与反应物分离的瓶颈的粒子的流(flux)。因此，在任何现代速率计算中的关键都是计算这个跨越瓶颈的流(归一化到单个粒子)。流遵循非平衡概率，该非平衡概率的边界条件为：在亚稳态内部，稳态平衡占优；在瓶颈区域之外，概率趋近于零，粒子立即被移除(或吸收)，然后重新注入到初始井中，产生稳态通量。在他的论文第237页，Farkas (1927)明确引入了这一关键概念，该概念如今作为flux-over-population(见Sec .Ⅱ. C)方法广为人知，他写道（从德文意译而来）

. . .In order to calculate for a diffusion problem the number of particles that go through a bottleneck one must know the concentration at two locations. In our case the diffusion process is not allowed to perturb the stationary distribution towards smaller particle numbers, (i.e., for numbers n ＜ n₀, with n₀ denoting the size of the critical nucleus); therefore one has an equilibrium concentration below (n ＜ n₀); above ( n ＞ n₀), however, one must have for very large n a vanishing concentration of droplets. .

​ 这里纳入了括号中的文本以澄清"下面"和"上面"的术语。随后，Farkas得到了成核速率的一个显式结果，该结果与后来由Becker和Doring ( 1935 )推广的结果一致。在此期间，化学家们并没有表现出惰性。20世纪初，Lindemann( 1922 )发展了单分子气相反应(或更一般的一级反应\(A\rightarrow B\) ，\(\dot c_A=-kc_A\), c表示浓度)的多步机理。此后不久，Hinshelwood (1926a, 1926b)等相继开发了定量方法。Fowler (1929)在他的著作Chap. XVIII中回顾了这个化学反应速率理论以及早期的双分子反应理论(或者更一般的二级反应, \(A + B\rightarrow C\) , \(\dot c_A=-k_{bim}c_Ac_B\))，Moelwyn-Hughes (1933)也综述了这些理论。

​ 接下来的重大发展再次来自化学物理学界。这体现于以下工作Polanyi和Wigner (1928), Pelzer和Wigner (1932), Evans和Polanyi (1935), Eyring (1935), 和Wynne-Jones 和Eyring (1935)。Polanyi和Wigner (1928) 和Eyring (1935)处理了由n个原子组成的分子非线性分解的情况。Eyring(1935)用可用势能面获得的量来表达速率，并分别对亚稳态(A)和活化复合物(≠)显式使用了(量子)统计的配分函数Z_A。这样他得出了一个划时代意义的速率公式(Eyring, 1935; Laidler and King, 1983), \[ k=\kappa[\frac{k_BT}{h} ]\frac{Z^\neq}{Z_A}exp(-\beta E_b)\equiv\kappa k_{TST} \tag{1.2} \] \(\kappa\)最初由Eyring ( 1935 )引入，作为一个特设的模糊因子(透射系数)，用于修正那些重新穿越过渡态回来(recross)且不分解返回的反应轨迹x(t)。显然，这一事实总是降低了反应速率k，使得\(\kappa \leq 1\)。在化学物理学界，这个方程(1.2)中的"大概念" (Grande Concept ) (Hirschfelder, 1982)是此后一直沿用、占统治地位的方法方法。其影响从Glasstone, Laidler和Eyring (1941)在他们的教科书中将这种近似理论称为"绝对率理论"可见一斑。例如，我们在这里提到，在计算热电子发射电流时，Richardson (1902, 1912), Laue (1918), and Dushman (1923)都隐式地使用了TST (参见Herzfeld, 1919)的简化的一维版本，其中一个具有功函数\(\phi\)的电子(则\(E_b \equiv e \phi\)) 在受周围晶格的动态影响的自由飞行中跨越了阈值势垒。

Hendrik Antonie Kramers (1894—1952) 早期从事反应速度理论研究。在1916年至1926年的哥本哈根期间，他与Christiansen (Christiansen and Kramers, 1923) 一起进行了关于单分子反应理论的研究。他们把玻尔兹曼碰撞理论和爱因斯坦的辐射理论结合起来，试图在能链机制内描述速率的指前因子。在经典的速率理论中，迄今为止所有后来的理论工作都聚焦于方程(1.1)中这个复杂的指前因子ν。1940年，Kramers以其著名的论文“Brownian Motion in a Field of Force and the Diffusion Model of Chemical Reactions" (Kramers, 1940) 回到了这一主题。他很好地理解了逃逸过程的机制就是噪声辅助反应。从推导相空间中非线性势场下布朗运动的Fokker - Planck方程[这在历史上早已由Klein ( 1922 )导出]出发，他将逃逸过程描绘为热力学力驱动的布朗运动动力学，通过波动耗散定理(fluctuation-dissipation theorem)这又与温度T和摩擦γ相关联。他分别分析了强摩擦和弱摩擦的情况。特别地，他在弱摩擦情况下的工作具有开创性：他首次导出了反应粒子的作用(action)(或能量)动力学的扩散方程。对于他的这一部分论文，他一定是以他早期的单分子气相反应工作为指导(Christiansen and Kramers, 1923),沿着先前Lindemann (1922), Christiansen (1926), 和 Hinshelwood (1926a)发展的路线工作。特别地，Polanyi (1920), Lewis和Smith (1925), Wigner (1925), Christiansen (1926), Hinshelwood (1926a, 1926b), 以及Polanyi和Wigner (1928) 都给出了单分子气相反应的速率： \[ k=\frac{\alpha}{(n-1)!}(\beta E_b)^{n-1}exp(-\beta E_b) \] 这里 n 表示强耦合振动模式的数量，α 表示碰撞频率，碰撞频率与压力（浓度）成正比。因此，在低压或弱摩擦情况下，公式 (1.3) 中的速率趋近于零。

​ Kramers 没有引用这些论文，但他一定是通过他所引用的Eyring以及Evans和Polanyi's(Evans and Polanyi, 1935; Eyring, 1935)的工作了解到这些发展。他的数学洞察力是非凡的。他的数学洞察力令人瞩目。他的确利用一些微妙的、近乎杂技的数学评估了极弱摩擦的逃逸率，从而证明了过渡态理论速率常数 \(k_{TST}\)严重高估了逃逸速率， \[ k(\gamma \rightarrow 0)=\gamma \beta I_bk_{TST}, \gamma \beta I_b \lt 1 \] 式中：I_b表示逃逸粒子在势垒处的作用(action)。此外，对于中强阻尼的情况，他成功地评估了二维相空间中的稳态非平衡概率流(\(x,\dot x=v\); 见Sec. IV)。在此过程中，他发明了一种巧妙的近似方案，将一个二元偏微分方程转化为一个常微分方程[见方程(4.24)-(4.26)]，从而得到方程(1.1)中指前因子ν的精华结果^[3]： \[ \nu=[[\frac{\gamma^2}{4}+\omega_b^2]^\frac{1}{2}-\frac{\gamma}{2}]\frac{\omega_0}{2\pi\omega_b}.\tag{1.5} \] 这里\(\omega^2_0 \equiv M^{-1}U^{''}(x_a)\)是亚稳态极小值点内部的角频率平方，\(\omega^2_0 \equiv M^{-1}|U^{''}(x_b)|\)是过渡态的角频率平方。在很长的一段时间了，他导出的Smoluchowski极限下的结果已被广为欣赏： \[ \nu=\stackrel{\gamma\gt \gt \omega_b}{\longrightarrow}\frac{\omega_b}{\gamma}\frac{\omega_0}{2\pi} \] 讽刺的是；在Kramers之前，过阻尼一维扩散逃逸动力学的这种情况实际上已经在Farkas (1927)，Kaischew和Stranski(1934)，以及Becker和Doring(1935)的论文中以更普遍的方式被解决，也考虑了状态依赖的扩散，，这些论文都涉及均相成核速率。Pontryagin, Andronov,和Vitt ( 1933 )通过计算一维Fokker - Planck过程的平均首次穿越时间也预期了过阻尼的结果。令人好奇的是，Kramers没有引用此前的任何工作。

​ 虽然Kramers的论文在标题中包含了"化学反应"一词，但当时的化学界并未直接使用他的预言。对于单分子气相反应，在Kramers 模型(见Sec. V)中，用离散的能量交换来描述速率比用连续的能量交换机制更合适。对于凝聚态化学反应，Kramers理论是最合适的，但这方面的工作需要等待七八十年代末取得的实验进展。同样地，最近才进行了非线性光学和凝聚态物理的实验，这些实验可以用Kramers的速率理论进行相当精确的解释(见Sec . XI)。这可能是Kramers提供的最优雅的方案的认可和欣赏非常缓慢的原因之一。自1940年以来，物理和化学之间仅发生了有限的交融。值得注意的是，最近非常权威的物理化学和动力学书籍( Berry , Rice , and Ross , 1980 ;Laidler, 1987)并没有讨论Kramers的结果。同样，很少有物理学家撰写的关于动力学或非平衡统计力学的著作讨论Polanyi和Wigner, Eyring等人开创的过渡态理论。事实上，在Eyring (1935)的工作之后，花了将近五十年的时间，才认识到具有记忆摩擦的Kramers理论(Grote和Hynes, 1980 , Hänggi and Mojtabai, 1982 ,Carmeli and Nitzan 1984, Straub、Borkovec, and Berne, 1985, 1986; Talkner and Braun, 1988)也能导出全相空间中所有自由度的多维过渡态理论(Hänggi, 1986a; Pollak 1986a, 1986b; Sec. III.C中也指出这一点)。幸运的是，二十年代物理学和化学之间曾经卓有成效的交融经历了复兴，从七十年代末开始，涉及关于(Chirikov, 1979; Pechukas, 1983; Casati, 1985)和反应速率量子理论(Miller, 1975; Wolynes, 1981; Caldeira and Leggett, 1981, 1983a, ' Weiss, Grabert, Hänggi, and Riseborough, 1987; Hänggi and Hontscha, 1988)的研究。

​ 在接下来的几部分中，我们试图回顾在1940年Kramers的历史奠基性论文之后五十年该领域的现状。目前的时间特别适合这样一个全面的回顾。在过去的二十年里，无论是在理论上还是在实验上，(除了大量的论文可以归类为重述, 或重新发现以前的发现)都产生了重要的新见解和深刻的发展。值得一提的不仅是上述Kramers理论的推广和具有记忆摩擦的速率理论的许多实际应用，而且还包括在弱摩擦(见Sec. V)，弱摩擦和强摩擦之间的转换(见Sec . VI)以及稳态非平衡速率理论(见Sec .Ⅷ)的最新进展。最近的许多令人兴奋的进展也产生了量子力学味道(见Sec .Ⅸ)。此外，最近在液体和约瑟夫森结系统中的实验速率研究为研究复杂情况下的速率过程提供了额外的动力。其他一些更为专门的综述性论文，在几个方面补充了我们的观点，并为本文所涉及的主题提供了更多的见解 Slater (1959), Troe (1975, 1986), Hase (1976), Pechukas (1976), Kapral (1981), Truhlar, Hase, and Hynes (1983), Hynes (1985, 1986a), Fonseca et al. (1985), Frauenfelder and Wolynes (1985), Chandler (1986), Fleming, Courtney, and Balk (1986), Hänggi (1986a, 1986b), Landauer (1987), Berne, Borkovec, and Straub (1988), Nitzan (1988), Sceats (1988), and Biittiker (1989)。

1. Logan (1982)、Laidler (1984, 1987)和Stiller (1989)给出了Arrhenius方程发展的美妙历史评论。审视Arrhenius的原文使得评论的作者们感到尴尬，他们认识到Arrhenius并未画出一条Arrhenius曲线，此外Arrhenius还将通常所谓的Arrhenius方程 (k=exp-(B/T)) 归功于Van't Hoff。然而，在他对速率数据的讨论中，他引入了一个"假想体"，即通常被称为"活化复合物"的活性状态，并提出了正常和活性反应物分子之间的平衡。这一概念本身无疑是对反应速度理论最重要的贡献。 ↩︎
2. 注意Farkas(1927)本人将他处理方法的基本思想归功于L.Szilard。 ↩︎
3. 见Kramers的(1940 )原文中方程(25)。注意Kramers(1940)用符号ω表示的不是角频率ω=2πν，而是频率ν本身。 ↩︎