Molecular Dynamics in NVE ensemble

热力学回顾

热力学基本方程 \[ dE=\delta Q+\delta W=TdS-pdV+\mu dN \] 特性函数 \[ S(N,V,E)=k_Bln \Omega(N,V,E) \]

\[ dS=\frac{1}{T}dE-\frac{p}{T}dV+\frac{\mu}{T}dN \]

N决定相空间的维度。V与边界条件相关，从量子力学来看，V与能级间距关联，从而影响态密度 \(\Omega\)。微正则系综的微观态分布于等能面 \(\hat H({\bf p,q})=E\) 上，概率分布为均匀分布。 配分函数即态密度(Density of State)是正则配分函数的拉普拉斯变换(Laplace Transformation) \[ \Omega(N,V,E) = \int_{E<\hat H({\bf p,q})<E+\Delta} \frac{d\Gamma}{h^{3N}N!}\delta (\hat H({\bf p,q})-E) \]

\[ P({\bf p,q})=\frac{\delta(\hat H({\bf p,q})-E)}{\Omega(N,V,E)} \]

可以用δ函数的性质证明位力定理(Virial theorem)，较为繁琐。 \[ <x_i\frac{\partial \hat H}{\partial x_j}>=k_BT\delta_{ij} \]

运动方程的积分算法

分子动力学的核心三要素是和运动方程积分算法、势函数模型、能量与力的计算。 经典力学运动方程的积分算法有许多，但并不是所有的算法都具有时间可逆性和辛性质（symplectic property）。时间可逆性即为时间反演可逆性，是说在某一时刻使时间轴反向，速度方向反转，则动力学系统会沿着原先的轨迹反向演化。例如我们令 $t'=-t $，则 \(\frac{d r}{d t}'=-\frac{d r}{d t}\), \(\frac{d^2 r}{d t'^2}=\frac{d^2 r}{d t}\),牛顿运动定律形式仍为 \(F=m\frac{d^2 r}{d t'^2}\)，这就意味着方程的时间可逆性。辛性质是说： 如果将Hamiltonian方程写成 \[ \dot x=M\frac{\partial \hat{H}}{\partial x} \]

其中 x 是相空间位矢，M是以下矩阵： \[ M=\begin{pmatrix} 0 & -I \\ I & 0 \end{pmatrix}\\ \] 其中 \(I\) 是3N×3N的单位矩阵，则对Jacobian矩阵(\(J_{k,l}=\frac{\partial x^k_t}{\partial x^l_0}\)): \[ M=J^TMJ \] 这意味着Jacobian行列式 \(|J|=1\)，相空间体积元守恒。这种性质确保了辛算法的积分误差有界，使得算法具有较好的数值稳定性，尤其是确保较好的能量守恒性。事实上存在对应于辛算法的依赖于时间步长 \(\Delta t\) 的Hamitolnian，在轨迹推进过程中该Hamitolnian精确守恒，步长较小时计算的能量与真实的能量偏离有限。

以下我们展示三种常用的时间可逆、具有辛性质的积分算法，并与不可逆的向前欧拉算法比较。我们首先基于Taylor展开推导这些算法的表达式。

1. Verlet 算法

\[ {\bf r_i}(t+\Delta t)={\bf r_i}(t)+{\bf v_i}(t)\Delta t+\frac{ {\bf F_i}(t)}{2m_i}{\Delta t}^2+\frac{ {\bf {r_i}'''}(t)}{6}{\Delta t}^3+O({\Delta t}^4) \]

\[ {\bf r_i}(t-\Delta t)={\bf r_i}(t)-{\bf v_i}(t)\Delta t+\frac{ {\bf F_i}(t)}{2m_i}{\Delta t}^2-\frac{ {\bf {r_i}'''}(t)}{6}{\Delta t}^3+O({\Delta t}^4) \]

两式相加，并移项可得 \[ {\bf r_i}(t+\Delta t)=2{\bf r_i}(t)-{\bf r_i}(t-\Delta t)+\frac{ {\bf F_i}(t)}{m_i}{\Delta t}^2+O({\Delta t}^4) \] 两式相减并移项： \[ {\bf v_i}(t+\Delta t)=\frac{ {\bf r_i}(t+\Delta t)-{\bf r_i}(t)}{2\Delta t}+O(\Delta t^2) \] 算法的实现： 1.初始化位置\(\{ {\bf r_i}(0)\}\)和速度\(\{ {\bf v_i}(0)\}\)。计算力\(\{ {\bf F_i}(0)\}\)，然后计算\(\{ {\bf r_i}(\Delta t)\}\)： \[ {\bf r_i}(\Delta t)={\bf r_i}(0)+{\bf v_i}(0)\Delta t+\frac{ {\bf F_i}(0)}{2m_i}{\Delta t}^2\tag{1.1} \] 2.将 t 设为当前时刻。计算\(\{ {\bf F_i}(t)\}\)，根据前两步的位置更新位置： \[ {\bf r_i}(t+\Delta t)=2{\bf r_i}(t)-{\bf r_i}(t-\Delta t)+\frac{ {\bf F_i}(t)}{m_i}{\Delta t}^2\tag{1.2} \] 3.动能(速度)需另外计算： \[ {\bf v_i}(t+\Delta t)=\frac{ {\bf r_i}(t+\Delta t)-{\bf r_i}(t)}{2\Delta t}\tag{1.3} \] 4.重复2、3步 可见Verlet算法中由于三阶项相互抵消位置的局部误差为四阶，对速度则为二阶。

2. 速度Verlet (Velocity Verlet)算法

\[ {\bf r_i}(t+\Delta t)={\bf r_i}(t)+{\bf v_i}(t)\Delta t+\frac{ {\bf F_i}(t)}{2m_i}{\Delta t}^2+O({\Delta t}^3) \]

\[ {\bf r_i}(t)={\bf r_i}(t+\Delta t)-{\bf v_i}(t+\Delta t)\Delta t+\frac{ {\bf F_i}(t+\Delta t)}{2m_i}{\Delta t}^2+O({\Delta t}^3) \]

两式相加消掉 \({\bf r_i}(t)\) 得： \[ {\bf v_i}(t+\Delta t)={\bf v_i}(t)+\frac{\Delta t}{2m_i}[{\bf F_i}(t)+{\bf F_i}(t+\Delta t)]+O(\Delta t^2) \] 相应算法为： 1.初始化位置\(\{ {\bf r_i}(0)\}\)和速度\(\{ {\bf v_i}(0)\}\)。

2. 将 t 设为当前时刻。计算力\(\{ {\bf F_i}(0)\}\)，然后根据式(1.1)更新位置。 3.计算 \({t+\Delta t}\) 时刻的力。 4.更新速度：

\[ {\bf v_i}(t+\Delta t)={\bf v_i}(t)+\frac{\Delta t}{2m_i}[{\bf F_i}(t)+{\bf F_i}(t+\Delta t)]\tag{2.1} \]

5. 重复2,3,4步。

3. 蛙跳法 (Leap Frog)算法

蛙跳法的特点在于，位置和速度的更新点总是间隔 \(1/2 \Delta t\)，形成在时间轴上位置和速度的轨迹相互交错。我们可以先更新半步速度： \[ {\bf v_i}(\frac{1}{2}\Delta t)={\bf v_i}(0)+{\bf F_i}(0)\frac{\Delta t}{2m_i}\tag{3.1} \] 令t为当前时刻，交替更新位置和速度： \[ {\bf r_i}(t+\Delta t)={\bf r_i}(t)+{\bf v_i}(t+\frac{\Delta t}{2})\Delta t\tag{3.2} \]

\[ {\bf v_i}(t+\frac{3}{2}\Delta t)={\bf v_i}(t+\frac{\Delta t}{2})+{\bf F_i}(t+\Delta t)\frac{\Delta t}{m_i}\tag{3.3} \]

在没有温度和压强耦合的情况下，给定相同的起始点，蛙跳法与速度Verlet方法产生相同的轨迹，它们都是位置的三阶算法。如果给定相同的初始坐标，并用相同的一组速度初始化Verlet算法的\(\{ {\bf v}(0)\}\)和蛙跳法的\(\{ {\bf v}(-\frac{\Delta t}{2})\}\)，则它们的轨迹相同。

4. 向前Euler算法

将微分方程 \({\bf \dot r_i}=\bf v_i\) 和 \({\bf \dot v_i}=\frac{\bf F_i}{m_i}\)分别展开到一阶： \[ {\bf r_i}(t+\Delta t)={\bf r_i}(t)+{\bf v_i}(t)\Delta t\tag{4.1} \]

\[ {\bf v_i}(t+\Delta t)={\bf v_i}(t)+\frac{\Delta t}{m_i}{\bf F_i}(t)\tag{4.2} \]

该算法对位置是二阶，对速度是一阶。从 \(t+\Delta t\) 时刻后退一步，得： \[ {\bf r_i'}(t)={\bf r_i}(t+\Delta t)-{\bf v_i}(t+\Delta t)\Delta t\\ =r_i(t)+[{\bf v_i}(t)-{\bf v_i}(t+\Delta t)]\Delta\\ =r_i(t)-\frac{\Delta t}{m_i}{\bf F_i}(t) \] 可见前向Euler算法不具有时间可逆性。一维体系单时间步的演化的Jacobian矩阵为： \[ J=\begin{pmatrix} \frac{\partial r_{t+\Delta t}}{\partial r_t} & \frac{\partial r_{t+\Delta t}}{\partial p_t} \\ \frac{\partial p_{t+\Delta t}}{\partial r_t} & \frac{\partial p_{t+\Delta t}}{\partial p_t} \end{pmatrix}\\ =\begin{pmatrix} 1 & \frac{\Delta t}{m} \\ \Delta t \frac{d F}{d r}|_{r=r(t)} & 1 \end{pmatrix}\\ \] 所以 \[ |J|=1-\frac{\Delta t^2}{m} \frac{d F}{d r}|_{r=r(t)}\neq 1 \] 前向Eular算法也不具有辛结构。

利用经典传播子(Classical Propagator)导出积分算法

考虑经典物理量 a，表达为相空间坐标的函数：\(a({\bf x}(t))\)，则其关于时间的全导数为： \[ \frac{d a}{d t}=\sum_{\alpha=1}^{3N}(\frac{\partial a}{\partial q_\alpha}\dot q_\alpha+\frac{\partial a}{\partial p_\alpha}\dot p_\alpha)\\ =\sum_{\alpha=1}^{3N}(\frac{\partial \hat H}{\partial p_\alpha}\frac{\partial a}{\partial q_\alpha}-\frac{\partial \hat H}{\partial q_\alpha}\frac{\partial a}{\partial p_\alpha}) \] 我们定义Lionville算符 \(i\hat L\)： \[ i\hat L=\sum_{\alpha=1}^{3N}(\frac{\partial \hat H}{\partial p_\alpha}\frac{\partial }{\partial q_\alpha}-\frac{\partial \hat H}{\partial q_\alpha}\frac{\partial }{\partial p_\alpha}) \] 有： \[ i\hat L a=\{a,\hat H\}=\frac{d a}{dt}\tag{5.1} \] 以上方程的形式解为： \[ a(t)=e^{i\hat L t}a(0) \] 对相空间位矢本身有： \[ {\bf x}(t)=e^{i\hat L t}{\bf x}(0) \tag{5.2} \] 其中 \(e^{i\hat L t}\) 即为经典传播子（量子传播子为 \(e^{-\frac{i\hat Ht}{\hbar}}\)）。如果令时间轴反转，则动量方向反转，含动量的微分反转，使得： \[ i\hat L'=-i\hat L \]

\[ x'(0)=e^{i \hat L't}x(t)=e^{-i \hat Lt}x(t)=x(0) \]

注：上式中的t是时间间隔，是常量。因此经典传播子对时间可逆。尽管有式(5.2)，算符对相空间位矢的解析表达式常常不能获得。我们将 \(i\hat L\) 拆分成 : \[i\hat L_1= \sum_{\alpha=1}^{3N}\frac{\partial \hat H}{\partial p_\alpha}\frac{\partial }{\partial q_\alpha}\tag{5.3}\] \[i\hat L_2= -\sum_{\alpha=1}^{3N}\frac{\partial \hat H}{\partial q_\alpha}\frac{\partial }{\partial p_\alpha}\tag{5.4}\] 然而由于这两个算符不对易，我们无法将传播子拆分： \[ e^{i \hat L}\neq e^{i \hat L_1}e^{i \hat L_2}\tag{5.5} \] 根据可逆Trotter定理，对任意算符 \(\hat A 、\hat B\)： \[ e^{\hat A+\hat B}=\lim_{P \to \infty}[e^{\frac{\hat B}{2P}}e^{\frac{\hat A}{P}}e^{\frac{\hat B}{2P}}]^P\tag{5.6} \] 其中 P 为正整数。如果我们令\(\Delta t=t/P\)，则： \[ e^{i\hat Lt}=\lim_{P \to \infty}[e^{\frac{i\hat L_2 \Delta t}{2}}e^{i\hat L_1\Delta t}e^{\frac{i\hat L_2 \Delta t}{2}}]^P \] 有限步数下： \[ e^{i\hat Lt}=[e^{\frac{i\hat L_2 \Delta t}{2}}e^{i\hat L_1\Delta t}e^{\frac{i\hat L_2 \Delta t}{2}}]^P+O(P\Delta t^3) \]

\[ e^{i\hat L\Delta t}= e^{\frac{i\hat L_2 \Delta t}{2}}e^{i\hat L_1\Delta t}e^{\frac{i\hat L_2 \Delta t}{2}}+O(\Delta t^3)\tag{5.7} \]

上式直接对应velocity Verlet算法。让我们考虑算符的形式与作用效果。对于Hamiltonian: \[\hat H=\sum_{i=1}^{N}\frac{\bf p_i^2}{2m_i}+U(\bf \{r_i\})\] \[ i\hat L_1=\sum_{i=1}^N\frac{\bf p_i}{m_i}\frac{\partial }{\partial \bf r_i}\tag{5.8} \]

\[ i\hat L_2=\sum_{i=1}^N {\bf F_i} \frac{\partial }{\partial \bf p_i}\tag{5.9} \]

这两个算符中求和的各项相互对易，从而它们的传播子作用效果相当于这种形式的算符：\(exp(c\frac{\partial}{\partial x})\) 分别作用于被操作函数上，其作用效果为： \[exp(c\frac{\partial }{\partial x})f(x)=\sum_{k=0}^{\infty}\frac{c^k}{k!}\frac{\partial^k f}{\partial x^k}=f(x+c)\tag{5.10}\] 因而velocity Verlet算法可表述为：1.速度(动量)更新半步 2. 位置更新整步 3. 更新力，然后计算整步后的速度。写成伪代码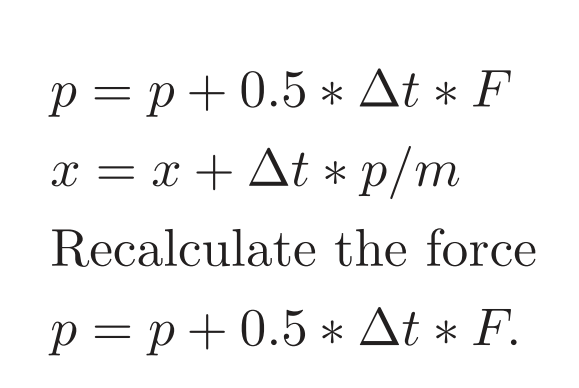： 可以证明这里所述的三步算法与前面的velocity Verlet算法相同。 传播子的不同构造方式导致了Verlet算法、蛙跳法，原则上它们的轨迹局部误差都是三价。在前述Verlet算法的实现中，所用步长相当于这里三步法中的一半，其局部误差为四阶。但就速度和位置都更新的完整一步而言，三种算法都是三价。它们的速度误差都是时间步长的二阶。 与温度与压力耦合时，更建议使用velocity Verlet算法。

image-20250207010749536

速度初始化

位置的初始化方式多样，选择合适的初始构型是分子模拟的重要议题，此处不讨论。正则系综、等温等压系综，粒子动量/速度的平衡态分布为Gaussian分布： \[ p(v_i)=\sqrt \frac{m_i}{2\pi k_BT}exp(-\frac{m_iv_i^2}{2k_BT})\tag{6.1} \] 其中 \(v_i\) 是分子 i 其中一个Cartesian坐标对应的速度。为了初始化粒子的速度，需产生符合上述分布的随机变量。产生符合特定概率分布的样本点也是Monte Carto的核心议题。

从已知概率分布和变换关系求未知分布

• 一维： 已知随机变量X具有概率分布函数(PDF) \(f_X(x)\)，设\(Y=g(X)\)，在定义域内X与Y一一对应，则Y的PDF为 \(f_Y(y)=f_X(g^{-1}(y))\cdot|\frac{dx}{dy}|\)。 证明如下 如果g(X)单调递增，则Y的累积分布函数CDF为

\[ F_Y(y)=P(Y\leqslant y)=P(g(X)\leqslant y)=P(X\leqslant g^{-1}(y))=F_X(g^{-1}(y)) \]

如果g(X)单调递减，则 \[ F_Y(y)=P(Y\leqslant y)=P(g(X)\leqslant y)=P(X\geqslant g^{-1}(y))=1-F_X(g^{-1}(y)) \] 则 \[ f_Y(y)=\pm\frac{dF_X[g^{-1}(y)]}{dy}=f_X(g^{-1}(y))\cdot|\frac{dx}{dy}|\tag{6.2} \]

• 二维及高维： 设随机变量组\((X_1,X_2)\)具有联合PDF \(f_{X_1X_2} (x_1,x_2)\)。通过可逆变换得到\((Y_1,Y_2)\)，在一定区域内\((X_1,X_2)\)与\((Y_1,Y_2)\)一一对应，其逆变换为：

\[ \begin{cases} X_1=w_1(Y_1,Y_2)\\X_2=w_2(Y_1,Y_2)\end{cases} \]

假设\((X_1,X_2)\)空间内任意区域\(\Gamma_X\)对应于\((Y_1,Y_2)\)空间内的\(\Gamma_Y\)，则\(P(\Gamma_X)=P(\Gamma_Y)\)，即 \[ \iint_{\Gamma_Y}f_{Y_1Y_2} (y_1,y_2)dy_1dy_2=\iint_{\Gamma_X}f_{X_1X_2} (x_1,x_2)dx_1dx_2\\=\iint_{\Gamma_Y}f_{X_1X_2} (w_1(y_1,y_2),w_2(y_1,y_2))|J|dy_1dy_2 \] 则 \[f_{Y_1Y_2} (y_1,y_2)=f_{X_1X_2} (w_1(y_1,y_2),w_2(y_1,y_2))|J|\tag{6.3}\] 其中|J|是Jacobian \[ |J|=\begin{vmatrix} \frac{\partial x_1}{\partial y_1} & \frac{\partial x_1}{\partial y_2} \\\\ \frac{\partial x_2}{\partial y_1} & \frac{\partial x_2}{\partial y_2} \end{vmatrix} \]

• 产生符合特定分布的随机变量 计算机通常能产生满足均匀分布的伪随机数。通过一定的变换，可将其转换满足任意概率分布的随机变量。如果 \(\zeta\) 满足[0,1]上均匀分布，\(p(x)\) 是目标概率分布，其CDF为\(F(x)\)。只要令\(F(X)=\zeta\)，即\(X=F^{-1}(\zeta)\)，就可使 \(X\) 具有目标概率分布 \(p(x)\)。

麻烦的是，Gaussian分布的CDF没有解析形式。而Box-Miller sampling提供了相对简单的获得Gaussian分布获取方式。考虑两个满足Gaussian分布的独立变量\(X\)、\(Y\)，其 PDF 为 \(f_{X,Y}(x,y)=\frac{1}{2\pi \sigma^2}exp(-\frac{x^2+y^2}{2\sigma^2})\)。其CDF为 \[F(x',y')=\frac{1}{2\pi \sigma^2}\int_{-\infty}^{x'} \int_{-\infty}^{y'} exp(-\frac{x^2+y^2}{2\sigma^2})dxdy\\ =\frac{1}{2\pi \sigma^2}\int_{0}^{\Phi'}d\Phi \int_{0}^{R'} R\,exp(-\frac{R^2}{2\sigma^2})dR\\ =\frac{\Phi}{2\pi}'[1-exp(-\frac{R'^2}{2\sigma^2})]\] 这里做了变换：

\[ \begin{cases} X=R\,cos\Phi\\ Y=R\,sin \Phi\end{cases} \]

上式最后一行可看做两个独立随机变量之CDF的乘积，令这两个随机变量为： \[ \begin{cases} \zeta_1=\Phi/2\pi\\ \zeta_2=1-exp(-\frac{R^2}{2\sigma^2})\end{cases} \] 这两个变量都是[0,1]上均匀分布的随机数，从而： \[ \begin{cases} X=\sigma \sqrt {-2ln(1-\zeta_2)}\,cos(2\pi\zeta_1)\\ Y=\sigma \sqrt {-2ln(1-\zeta_2)}\,sin(2\pi\zeta_1)\end{cases} \tag{6.4} \] 对于速度分布 \(\sigma=\sqrt{\frac{k_BT}{m_i}}\).

模型体系

一维简谐振子

\[ \hat H=\frac{p^2}{2m}+\frac{1}{2}m\omega^2x^2\tag{7.1} \]

Hamiltonian 正则方程为 \[ \begin{cases}\dot p=-m\omega^2x\\\dot x=p/m\end{cases}\tag{7.2} \] 解之得： \[ \begin{cases}x(t)=x(0)cos(\omega t)+\frac{p(0)}{m\omega}sin(\omega t)\\p(t)=-m\omega \cdot x(0)sin(\omega t)+p(0)cos(\omega t)\end{cases} \tag{7.3} \] 相空间轨迹为一个椭圆： \[ \frac{[p(t)]^2}{2m}+\frac{1}{2}m\omega^2[x(t)]^2=E\tag{7.4} \] 总能 \[ E=\frac{[p(0)]^2}{2m}+\frac{1}{2}m\omega^2[x(0)]^2 \] 代码实现（输入模型参数和初始坐标、动量，模拟步数和步长。输出轨迹、对应点的动量和能量）：

#简谐振子
import numpy as np
import matplotlib.pyplot as plt
from math import cos,sin,sqrt
def oscillator(x0,p0,n,dt,m,omega):
    trj=np.zeros([3,n+1])
    e0=p0*p0/2/m+0.5*m*omega*omega*x0*x0
    trj[:,0]=[x0,p0,e0]
    for i in np.arange(1,n+1):
        t=i*dt
        x=x0*cos(omega*t)+p0/m/omega*sin(omega*t)
        p=-m*omega*x0*sin(omega*t)+p0*cos(omega*t)
        e=p*p/2/m+0.5*m*omega*omega*x*x
        trj[:,i]=[x,p,e]
    return trj
def int_euler(x0,p0,n,dt,m,omega):
    trj=np.zeros([3,n+1])
    e0=p0*p0/2/m+0.5*m*omega*omega*x0*x0
    x=x0
    p=p0
    trj[:,0]=[x0,p0,e0]
    for i in np.arange(1,n+1):
        f=-m*omega*omega*x
        x=x+p/m*dt
        p=p+f*dt
        e=p*p/2/m+0.5*m*omega*omega*x*x
        trj[:,i]=[x,p,e]
    return trj
def int_verlet(x0,p0,n,dt,m,omega):
    trj=np.zeros([3,n+1])
    e0=p0*p0/2/m+0.5*m*omega*omega*x0*x0
    x=x0
    p=p0
    trj[:,0]=[x0,p0,e0]
    for i in np.arange(1,n+1):
        x=x+p/m*dt/2
        f=-m*omega*omega*x
        p=p+f*dt
        x=x+p/m*dt/2
        e=p*p/2/m+0.5*m*omega*omega*x*x
        trj[:,i]=[x,p,e]
    return trj
def int_vverlet(x0,p0,n,dt,m,omega):
    trj=np.zeros([3,n+1])
    e0=p0*p0/2/m+0.5*m*omega*omega*x0*x0
    x=x0
    p=p0
    f=-m*omega*omega*x
    trj[:,0]=[x0,p0,e0]
    for i in np.arange(1,n+1):
        p=p+f*dt/2
        x=x+p/m*dt
        f=-m*omega*omega*x
        p=p+f*dt/2
        e=p*p/2/m+0.5*m*omega*omega*x*x
        trj[:,i]=[x,p,e]
    return trj
def int_leapfrog(x0,p0,n,dt,m,omega):
    #速度(动量)从0.5dt时刻算起，n是位置步的数目
    trj=np.zeros([3,n+1])
    x=x0
    f=-m*omega*omega*x
    p=p0+f*dt/2
    e0=p0*p0/2/m+0.5*m*omega*omega*x0*x0
    trj[:,0]=[x,p,e0]
    for i in np.arange(1,n+1):
        k0=p*p/2/m
        x=x+p/m*dt
        f=-m*omega*omega*x
        p=p+f*dt
        #t时刻的动能用t-dt/2和t+dt/2的平均得到
        kn=(p*p/2/m+k0)/2
        e=kn+0.5*m*omega*omega*x*x
        #动量所对应的时刻与位置的时刻错开
        trj[:,i]=[x,p,e]
    return trj

结果：

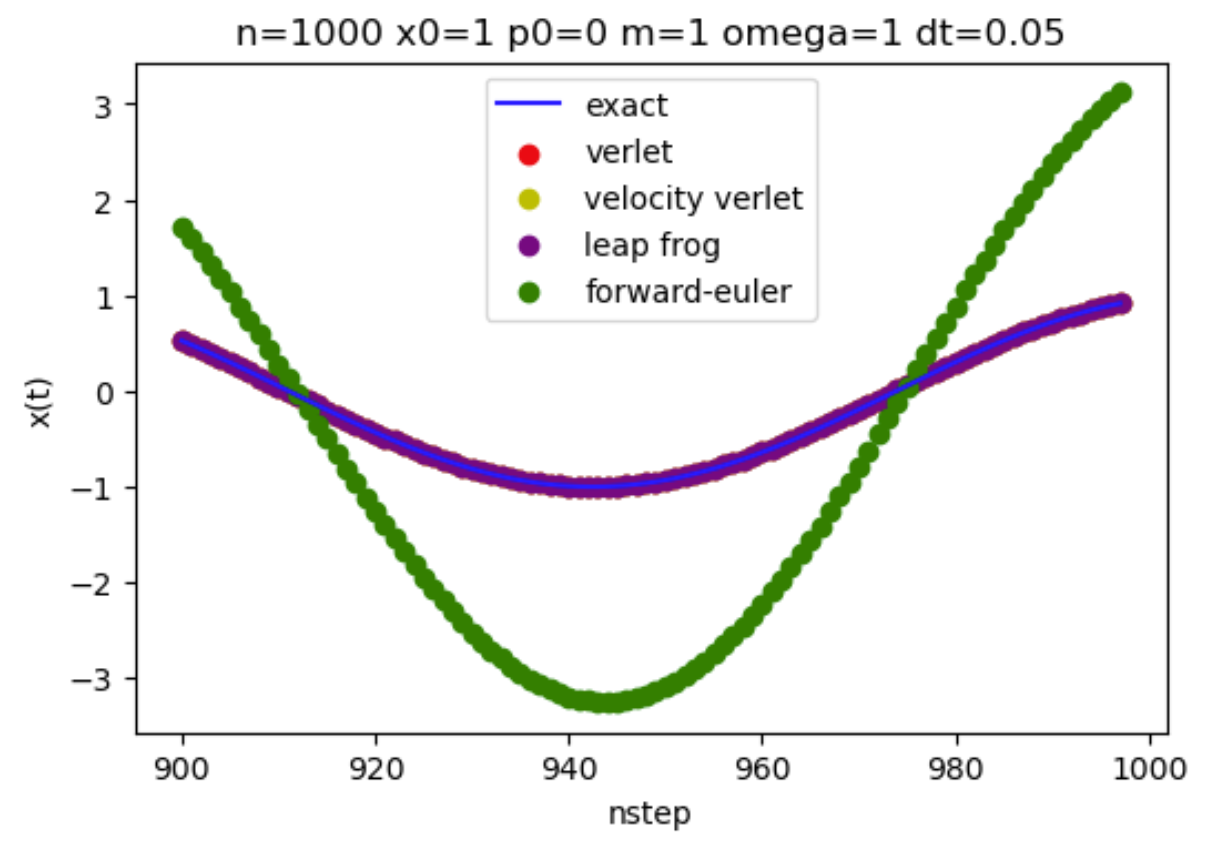
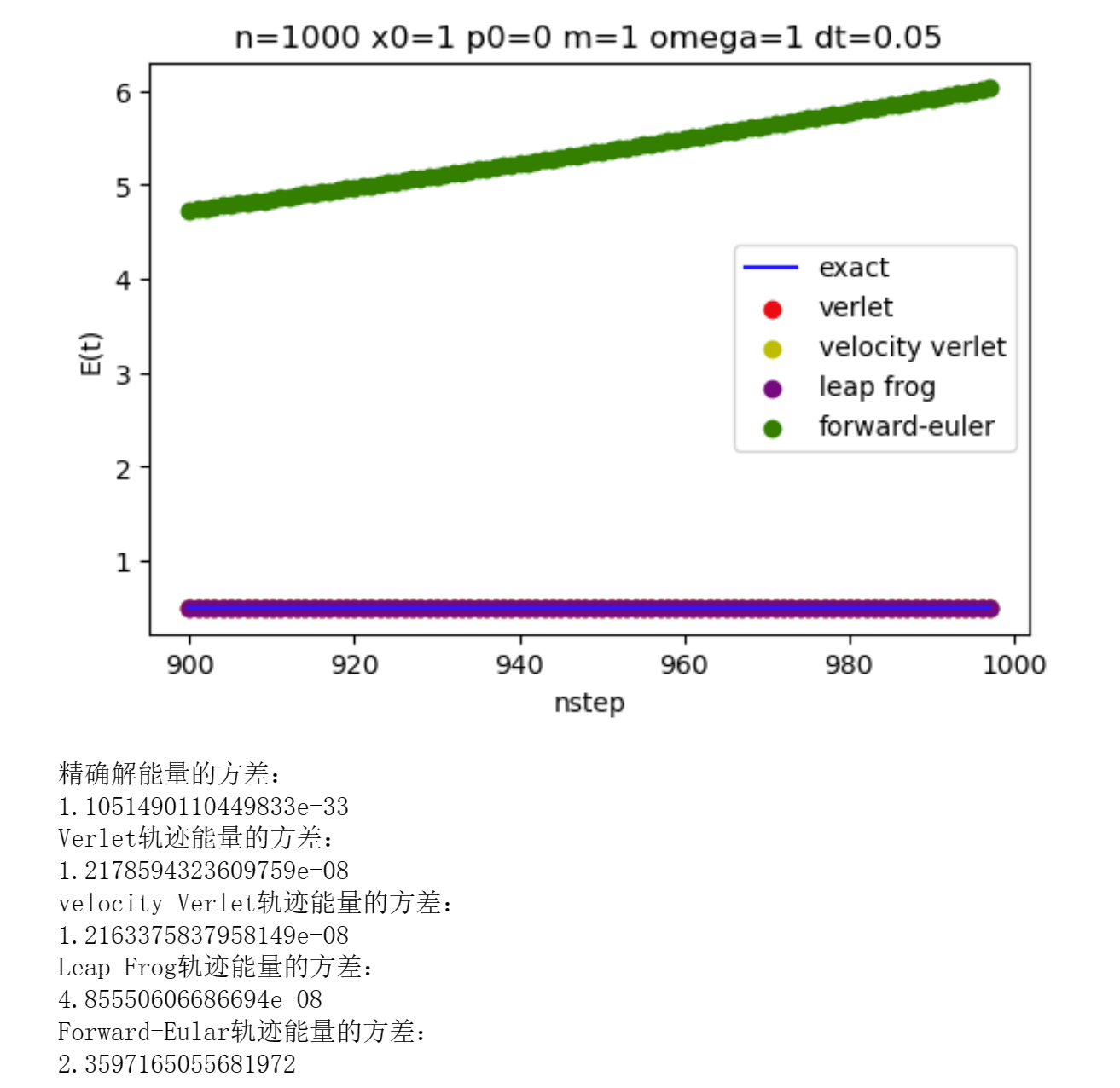
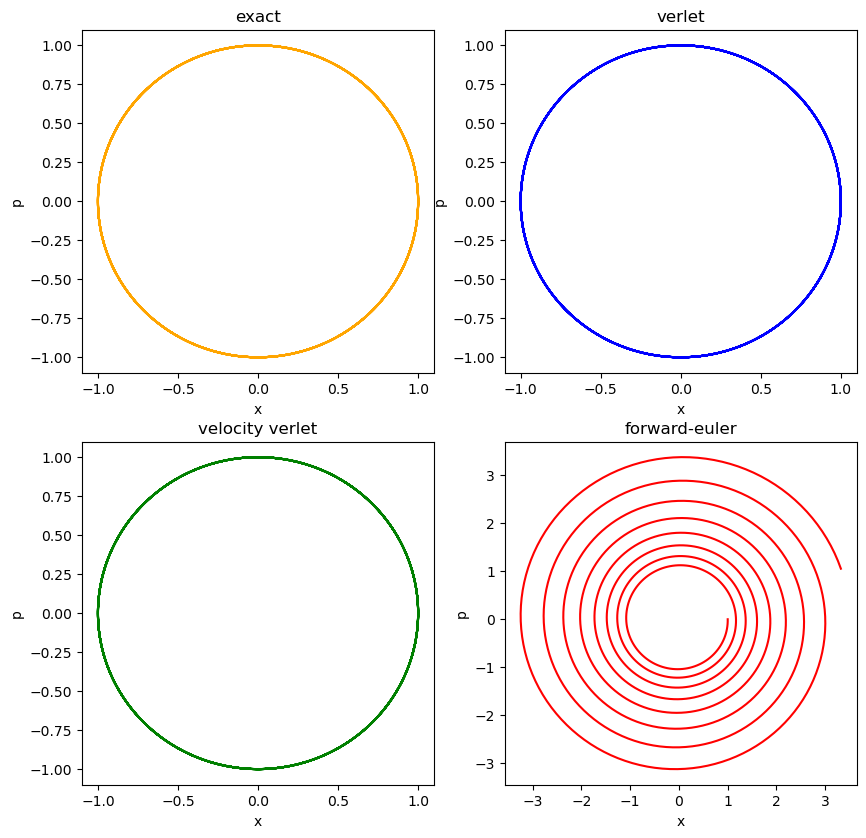
可见在当前步长下，向前Euler算法不能保证能量守恒，数值稳定性不佳，模拟过程中相轨迹发散（能量增大)。相比之下辛算法的能量守恒性很好。

参考文献

1. Mark E. Tuckerman. (2010). Statistical Mechanics: Theory and Molecular Simulation. Oxford: Oxford University Press.