Basis of Statistical Mechanics in Equilibrium Ensemble
一个宏观系统的具有数目庞大的自由度,可能的微观态(microstate)有许多。在通常的时间尺度下对系统进行观测,系统每一时刻都处于某个微观态,在不同的微观态之间切换,观测所得的物理量是不同微观态的时间平均: \[ \overline O = \frac{1}{t_0}\int_0^{t_0} O(t)dt\, = \sum_i^Nf(\mu_i) O(\mu_i). \tag{1.1} \] 如果系统处于各个微观态的概率不随时间变化,即稳态概率分布,且观测时间足够长,系统能够遍历一切可能的微观态并采样到正确的概率分布,则上述时间平均可以写成以概率为权重,对各个微观态性质的加权平均: \[ <O> = \sum_i^Np(\mu_i) O(\mu_i) \tag{1.2}. \] 为得到概率分布,想象许多个当前系统的思维副本所构成的集合——系综(ensemble),使其成员各自独立地按相同的运动方程演化,根据大数定律,当副本数目趋向无穷(热力学极限),就能采样到正确的稳态概率分布。如果前述各态历经(ergodicity)假设成立,我们就可以用式(1.2)的系综平均代替式(1.1)的时间平均,避免直接求解含~1023个粒子的宏观体系的运动方程,用统计的方法从微观粒子的力学性质计算宏观物理量。
经典相空间(Classical Phase space)
在经典力学中,一个N粒子系统的微观状态可以完全由每个粒子的空间坐标
\(\vec{q_i}\) 和动量 \(\vec{p_i}\)
确定,所有可能的微观态组成6N维的相空间(phase space) \(\Gamma = \Pi_{i=1}^N
\{\vec{q_i},\vec{p_i}\}\)
。对保守体系,相点的轨迹可由哈密顿方正则方程(canonical equations)描述:
\[
\begin{cases} \frac{d\vec{q_i}}{dt}=\frac{\partial \hat{\cal
H}}{\partial \vec{p_i}}\\\frac{d\vec{p_i}}{dt}=-\frac{\partial \hat{\cal
H}}{\partial \vec{q_i}}\end{cases} \tag{1.3}
\]
注意它具有时间反演对称性,即在某一时刻如果动量大小不变,方向反转,体系会演原先轨迹演化。系综可视为相空间中满足一定边界条件(Boundary
Conditions)和约束(Constrains)区域内的大量点的集合,系综中的每个成员都对应于相空间中一个代表点
\(\mu_i(t)\),系统处于某一点\((\mathbf{p},\mathbf{q})\)附近的概率为:
\[
\rho(\mathbf{p},\mathbf{q},t) d\Gamma= \lim_{N\to \infty}
\frac{dN(\mathbf{p},\mathbf{q},t)}{N}. \tag{1.4}
\] 系综平均为: \[
<O>=\int
\rho(\mathbf{p},\mathbf{q},t)O(\mathbf{p},\mathbf{q})d\Gamma . \tag{1.5}
\] 这样系统的宏观态可由相空间密度 \(\rho(t)\)
来描述,密度随时间的演化遵循刘维尔定理(Liouville's equation)
,可由任何一对代表点所围成的体积不随时间变化来证明:
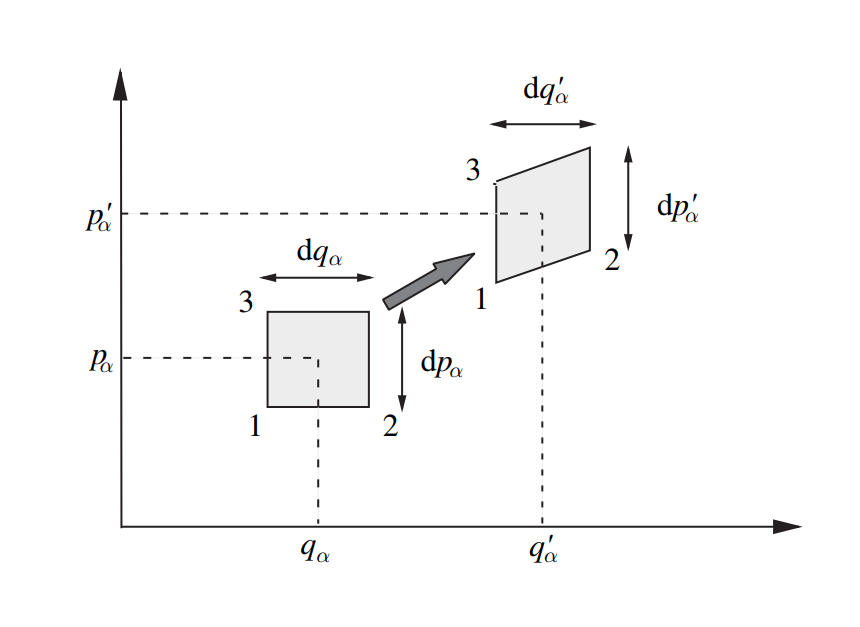 \[
\frac{d\rho}{dt} = \frac{\partial \rho}{\partial t} +
\sum_{a=1}^{3N}(\frac{\partial \rho}{\partial
p_{\alpha}}\cdot\frac{dp_\alpha}{dt}+\frac{\partial \rho}{\partial
q_\alpha}\cdot\frac{dq_\alpha}{dt}) = 0. \tag{1.6}
\]
这说明相空间密度的行为如同不可压缩流体,若随着某一个流体质点运动,经过的区域流体密度不发生改变。也可表述为N个代表点所占据的相空间体积不随时间变化(这似乎说明系统的微观态对应于相空间内的固定体积)。
引入泊松括号: \[
\{A, B\}=\sum_{a=1}^{3N}(\frac{\partial A}{\partial
q_{\alpha}}\cdot\frac{\partial B}{\partial p_\alpha}-\frac{\partial
A}{\partial p_\alpha}\cdot\frac{\partial B}{\partial q_\alpha}) =
-\{B,A\}. \tag{1.7}
\] 根据正则方程,式(1.6)可写成: \[
\frac{\partial \rho}{\partial t} = -\{\rho, \hat{\cal H}\} \tag{1.8}
\]
该方程同样具有时间反演对称性。由该方程可推出物理量的系综平均随时间的变化率为
\[
\frac{d<O>}{dt}=<\{O, \hat{\cal H}\}> \tag{1.9}
\] 平衡态下系综平均不随时间变化,系综具有稳态的密度:\(\partial \rho_{eq}/\partial t=0\),则\(\{\rho_{eq}, \hat{\cal
H}\}=0\)。该方程一个自然的解为:\(\rho_{eq}(\mathbf{p},\mathbf{q})=\rho(\hat{\cal
H}(\mathbf{p},\mathbf{q}))\),即 \(\rho\) 显含 \(\hat{\cal H}\) 且表示为只是 \(\hat{\cal H}\) 的单变量函数,在恒能面 \(\hat{\cal H}(\mathbf{p},\mathbf{q})=E\) 上
\(\rho\) 为常数 。
平衡态下能量相同的微观态出现概率相同,这构成了统计力学的等概率公设(Postulate
of Equal a Priori Probability)。如果相空间密度具有 \(\rho=\rho(\hat{\cal H}(\mathbf p, \mathbf
q),L_1(\mathbf p,\mathbf q),L_2(\mathbf p,\mathbf q),...)\)
的形式,\(L_n\) 是满足 \(\{L_n,\hat{\cal H}\}=0\) 的守恒量,则 \(\rho\) 也是稳态密度。
\[
\frac{d\rho}{dt} = \frac{\partial \rho}{\partial t} +
\sum_{a=1}^{3N}(\frac{\partial \rho}{\partial
p_{\alpha}}\cdot\frac{dp_\alpha}{dt}+\frac{\partial \rho}{\partial
q_\alpha}\cdot\frac{dq_\alpha}{dt}) = 0. \tag{1.6}
\]
这说明相空间密度的行为如同不可压缩流体,若随着某一个流体质点运动,经过的区域流体密度不发生改变。也可表述为N个代表点所占据的相空间体积不随时间变化(这似乎说明系统的微观态对应于相空间内的固定体积)。
引入泊松括号: \[
\{A, B\}=\sum_{a=1}^{3N}(\frac{\partial A}{\partial
q_{\alpha}}\cdot\frac{\partial B}{\partial p_\alpha}-\frac{\partial
A}{\partial p_\alpha}\cdot\frac{\partial B}{\partial q_\alpha}) =
-\{B,A\}. \tag{1.7}
\] 根据正则方程,式(1.6)可写成: \[
\frac{\partial \rho}{\partial t} = -\{\rho, \hat{\cal H}\} \tag{1.8}
\]
该方程同样具有时间反演对称性。由该方程可推出物理量的系综平均随时间的变化率为
\[
\frac{d<O>}{dt}=<\{O, \hat{\cal H}\}> \tag{1.9}
\] 平衡态下系综平均不随时间变化,系综具有稳态的密度:\(\partial \rho_{eq}/\partial t=0\),则\(\{\rho_{eq}, \hat{\cal
H}\}=0\)。该方程一个自然的解为:\(\rho_{eq}(\mathbf{p},\mathbf{q})=\rho(\hat{\cal
H}(\mathbf{p},\mathbf{q}))\),即 \(\rho\) 显含 \(\hat{\cal H}\) 且表示为只是 \(\hat{\cal H}\) 的单变量函数,在恒能面 \(\hat{\cal H}(\mathbf{p},\mathbf{q})=E\) 上
\(\rho\) 为常数 。
平衡态下能量相同的微观态出现概率相同,这构成了统计力学的等概率公设(Postulate
of Equal a Priori Probability)。如果相空间密度具有 \(\rho=\rho(\hat{\cal H}(\mathbf p, \mathbf
q),L_1(\mathbf p,\mathbf q),L_2(\mathbf p,\mathbf q),...)\)
的形式,\(L_n\) 是满足 \(\{L_n,\hat{\cal H}\}=0\) 的守恒量,则 \(\rho\) 也是稳态密度。
系综理论(Ensemble Theory)
平衡态统计力学的基本假设
- 遍历假设(ergodicity): 物理量 \(f\) 的观测值 = 长时间平均 \(\frac{1}{\Delta t}\int_0^{\Delta t}f(t)dt\) = 系综平均\(<f>\)。 这就要求在观测时间内,系统能到达所有可能的微观态,并无偏地采样到平衡态的概率分布。对于少数体系,可证明遍历性定理(ergodic theorem),充分长的时间内代表点可无限接近相空间内所有的可及点,然而该时间尺度远远大于通常观测的时间。实际情况下环境的微扰会大大增加系统到达各可能状态的能力。各态历经假设的合理性只能通过实验证明。
- 等概率公设 (Boltzmann's assumption of equal a priori equilibrium probabilities): 平衡态的孤立体系各微观状态等几率出现。在经典相空间中,等能面上的概率密度均匀分布。
- 熵(entropy)的统计定义: 孤立体系的熵为 \[ S=k_Bln\Omega \tag{1.10} \] 其中 \(k_B\) 是Boltzmann常数,\(\Omega\) 是体系可能的微观状态数。式(1.10)定义的熵等价于信息论中均匀概率分布的信息熵。熵是无序性与信息不确定性的量度,系统内部的自发过程总是倾向使系统的熵增大(满足约束条件下系综概率分布的重组亦可视为“内部自发过程”)。平衡态使熵取极大值。
信息熵 考虑离散的随机变量 \(X=\{x_i\}\),每种可能输出的出现概率为 \(\{p_i\}, i=1,2,...,M.\) 若进行 N 次独立重复试验,结果有MN种可能的情况,如果没有任何关于试验结果的先验知识,则精确地传达试验结果需要 \(Nlog_2M\) bit的信息。现在知道随机变量 X 输出值的概率分布,如果各种输出的出现概率不均等,则实验结果的不确定性减少。当 \(N\to\infty\),可认为 N 次试验中,xi 出现次数为Ni=Npi 。这样可能的序列数为: \[ \Omega=\frac{N!}{\prod_{i=1}^MN_i!} \tag{1.11} \] 指定试验结果序列需要的信息量(使用Starling近似): \[ log_2 {\Omega}\approx-N\sum_{i=1}^Mp_ilog_2{p_i} \quad (for \quad N\to\infty) \tag{1.12} \] Shannon定理指出,这就是N趋于无穷的极限下精确传递信息所需的最少bit数。 非均匀概率分布 \(log_2\Omega\) 小于 \(Nlog_2M\) ,这就说明概率分布本身携带信息,使得结果的不确定性减小,其信息量定义为: \[ I[\{p_i\}]=log_2M+\sum_{i=1}^Mp_ilog_2{p_i} \tag{1.13} \] 除了 \(\delta\) 函数分布 \(p_i=\delta_{i,j}\)外,其余的概率分布仍存在不确定性,需要大于1bit的信息确定试验结果,式(1.12)的量度量了这种不确定性。我们定义概率分布的信息熵为: \[ S=-\sum_{i=1}^Mp_ilnp_i=-<lnp> \tag{1.14} \] \(\delta\) 函数分布的熵为0,而均匀分布 \(p_i=1/M\) 的熵取最大值\(lnM\)。S 是概率分布离散性的量度,是无序性和不确定性的量度。信息论的熵定义对所有系综均适用,均匀分布的情况(孤立体系),信息熵等同于Boltzmann熵。 遍历假设使我们不必研究宏观系统的含时演化,转而研究各微观态上概率分布。平衡系统的宏观态M与相空间的概率密度函数 \(\rho_M(\bf q,\bf p)\) 或希尔伯特空间的密度矩阵 \(\bf {\rho_M}\) 一一对应,只要知道后者,就能计算宏观系统的一切物理量。系综理论的核心就在于推导各种系综的概率分布函数。大致有三种方式:(1) 研究与环境达到热平衡的系统,复合系统形成孤立体系 (2) 最概然分布法。利用Lagrange乘子法求取满足系综约束条件并使Boltzmann熵或信息熵最大的概率分布。(3) Darwin-Fowler 鞍点法。
系统-环境法
最概然分布法
微正则系综(Microcanonical Ensemble)
微正则系综对应于孤立体系,系统的粒子数 N、体积 V (广义位移x)和能量 E 固定,其宏观状态即由这组参数 \((N,V,E)\) 唯一确定 。根据基本假设,系统处于某一微观态 \(\mu\) 的概率为: \[ p(\mu)=\frac{\delta(\hat{\cal H}(\mu)-E)}{\Omega(N,V,E)}\tag{1.15} \] 经典相空间中的密度为: \[ \rho(\mathbf p, \mathbf q)= \frac{\delta_\Delta(\hat{\cal H}(\mathbf p,\mathbf q)-E)}{\Omega(N,V,E)}\tag{1.16} \] 其中 \(\Omega(N,V,E)\) 是满足边界条件和约束条件:\(E-\Delta \le \hat{\cal H}(\mathbf p,\mathbf q)\le E+\Delta\) 的区域体积。显然相空间体积与微观状态数对应。由于量子力学中的不确定性关系,动量 p 和位置 q 不可同时精确确定。 微观状态数应是与单位无关的无量纲量,而相空间体积元具有(动量×长度)3N的量纲。并考虑全同粒子的不可分辨性,相空间体积元应校正为: \[ d\Gamma_N=\frac{1}{h^{3N}N!}\prod_{i=1}^Nd^3\vec q_id^3\vec p_i \tag{1.17} \] 从信息熵的定义出发,可自然地推导出微正则系综的均匀概率分布。
拉格朗日乘子法(Lagrange Multiplier Method)
拉格朗日乘子法用于解决带约束条件下的优化问题,其基本思想是通过引入拉格朗日乘子,将含有n个变量、k个约束条件的约束优化问题转化为含(n+k)个变量的无约束优化问题。
首先考虑只有单个等式约束的优化问题: \[
\begin{align} min \quad &f(\mathbf x) \\
s.t. \quad &g(\mathbf x)=0 \quad \end{align}\tag{1.18}
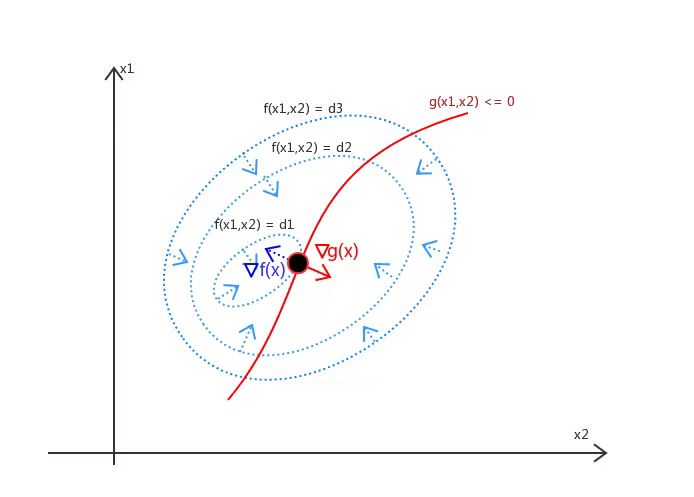
\] 目标是在由方程 \(g(\mathbf
x)=0\) 确定的 (n-1) 维曲面上寻找极值点,从几何上说,该点处 \(f(\mathbf x)\)
的等值面与约束曲面相切,使得沿约束曲面的任意切线方向 \(f(\mathbf x)\)
的方向导数都为零。约束曲面的任一点处梯度 \(\nabla g(\mathbf x)\) 都与曲面正交,\(f(\mathbf x)\) 的等值面上 \(\nabla f(\mathbf
x)\)也正交于切面。因而在最优点,此两者应当共线: \[
\nabla f(\mathbf x)+\lambda \nabla g(\mathbf x)=0 \tag{1.19}
\] 上式有n个方程,加上约束等式即可确定最优点坐标 \(\bf x^*\) 和Lagrange乘子\(\lambda\)。若无约束条件下的 \(f(\mathbf x)\) 极值点恰在约束曲面上,则
\(\nabla f(\mathbf x^*)=0\),设\(\lambda=0\),式 (1.19) 仍成立.
定义Lagrange函数 \(L(\mathbf
x,\lambda)=f(\mathbf x)+\lambda g(\mathbf
x)\),则等式约束的极值条件写成: \[
\begin{align}\nabla_{\mathbf x} L(\mathbf x,\lambda)=0\Leftrightarrow
\nabla f(\mathbf x)+\lambda \nabla g(\mathbf x)=0 \\
\frac{\partial L(\mathbf x,\lambda)}{\partial \lambda}=0 \Leftrightarrow
g(\mathbf x)=0 \quad \end{align}\tag{1.20}
\] 上述方法可推广到多个等式约束的情形,此时 \(\nabla f(\mathbf x)\)
是各个约束方程梯度的线性组合: \[\begin{align}\lambda_ig_i(\mathbf x)=0 \quad
i=1,2,...,k\\
\nabla f(\mathbf x)+\sum_{i=1}^k\lambda_i \nabla g_i(\mathbf x)=0
\end{align}\tag{1.21}\]
Lagrange乘子法也适用于不等式约束。考虑约束条件 \(g(\mathbf x)\le0\),最优点要么在 \(g(\mathbf x)\lt0\) 的区域内,要么在边界
\(g(\mathbf x)=0\) 上。第一种情况可令
\(\nabla f(\mathbf x)=0\),等价于\(\lambda=0\)时对Lagrange函数求导。后一种情况类似等式约束的处理,但附加
\(\nabla f(\mathbf x^*)\) 与 \(\nabla g(\mathbf x^*)\)
方向相反的条件,即\(\lambda>0\),否则边界附近以内的区域存在比边界上函数值更小的点,最优点不在边界上。
 对于含同时含等式和不等式约束的优化问题,Lagrange乘子法可将原始问题转化为Karush-Kuhn-Tucker条件(KKT)条件下Lagrange函数的最优化问题。KKT条件是转化后问题与原问题等价的必要条件。
原问题: \[
\begin{align} min \quad &f(\mathbf x)\\
s.t.: \,\quad &g_i(\mathbf x)\le0\quad i=1,...,m \\
\quad\qquad &h_j(\mathbf x)=0\quad j=1,...,l \end {align} \tag{1.22}
\] Lagrange乘子: \[
\begin{align}min\quad L(\mathbf x,\mathbf \lambda,\mathbf
\mu)&=f(\mathbf x)+\sum_{i=1}^m\lambda_ig_i(\mathbf
x)+\sum_{j=1}^l\mu_jh_j(\mathbf x)\\
-\nabla f(\mathbf x^*)&=\sum_{i=1}^m\lambda_i \nabla g_i(\mathbf
x^*)+\sum_{j=1}^l\mu_j \nabla h_j(\mathbf x^*) \Leftrightarrow
\nabla_{\mathbf x}L(\mathbf x^*,\mathbf \lambda,\mathbf \mu)=0 \\
KKT \quad conditions:\\
\,\,\,\,\quad g_i(\mathbf x^*)&\le0\quad i=1,...,m\\
\mu_jh_j(\mathbf x^*)&=0\quad j=1,...,l \\
\quad \qquad \lambda_i&\ge0\quad i=1,...,m\\
\,\, \lambda_ig_i(\mathbf x^*)&=0 \quad i=1,...,m
\end{align}\tag{1.23}
\] Example —— 最大化离散分布的信息熵
假设有一组随机变量 \(S=\{s_1,s_2,...s_n\}\), 对应的概率分布为
\(\mathbf p=\{p_1,p_2,...,p_n\}\),
求最大化信息熵的概率分布。该问题可表述为在概率归一化条件的约束下n个变量的优化问题:
\[
\begin{align}max \quad S(p_1,...,p_n)&=-\sum_{i=1}^np_ilnp_i\\
s.t. \quad \sum_{i=1}^np_i-1&=0\end{align}\tag{1.24}
\] 定义Lagrange函数: \[
L(p_1,...p_n,
\lambda)=S(p_1,...,p_n)+\lambda(\sum_{i=1}^np_i-1)\tag{1.25}
\] 极值条件为以下n+1个方程: \[
\begin{align}\frac{\partial L}{\partial
p_i}&=-(lnp_i+1)+\lambda=0\quad i=1,...,n\\
\frac{\partial L}{\partial \lambda}&=
\sum_{i=1}^np_i-1=0\end{align}\tag{1.26}
\] 则 \(p_1=\cdots
=p_n=\frac{1}{n},\lambda=1-ln{\,n}\).
可见无其他约束条件下,均匀分布使信息熵最大化。
对于含同时含等式和不等式约束的优化问题,Lagrange乘子法可将原始问题转化为Karush-Kuhn-Tucker条件(KKT)条件下Lagrange函数的最优化问题。KKT条件是转化后问题与原问题等价的必要条件。
原问题: \[
\begin{align} min \quad &f(\mathbf x)\\
s.t.: \,\quad &g_i(\mathbf x)\le0\quad i=1,...,m \\
\quad\qquad &h_j(\mathbf x)=0\quad j=1,...,l \end {align} \tag{1.22}
\] Lagrange乘子: \[
\begin{align}min\quad L(\mathbf x,\mathbf \lambda,\mathbf
\mu)&=f(\mathbf x)+\sum_{i=1}^m\lambda_ig_i(\mathbf
x)+\sum_{j=1}^l\mu_jh_j(\mathbf x)\\
-\nabla f(\mathbf x^*)&=\sum_{i=1}^m\lambda_i \nabla g_i(\mathbf
x^*)+\sum_{j=1}^l\mu_j \nabla h_j(\mathbf x^*) \Leftrightarrow
\nabla_{\mathbf x}L(\mathbf x^*,\mathbf \lambda,\mathbf \mu)=0 \\
KKT \quad conditions:\\
\,\,\,\,\quad g_i(\mathbf x^*)&\le0\quad i=1,...,m\\
\mu_jh_j(\mathbf x^*)&=0\quad j=1,...,l \\
\quad \qquad \lambda_i&\ge0\quad i=1,...,m\\
\,\, \lambda_ig_i(\mathbf x^*)&=0 \quad i=1,...,m
\end{align}\tag{1.23}
\] Example —— 最大化离散分布的信息熵
假设有一组随机变量 \(S=\{s_1,s_2,...s_n\}\), 对应的概率分布为
\(\mathbf p=\{p_1,p_2,...,p_n\}\),
求最大化信息熵的概率分布。该问题可表述为在概率归一化条件的约束下n个变量的优化问题:
\[
\begin{align}max \quad S(p_1,...,p_n)&=-\sum_{i=1}^np_ilnp_i\\
s.t. \quad \sum_{i=1}^np_i-1&=0\end{align}\tag{1.24}
\] 定义Lagrange函数: \[
L(p_1,...p_n,
\lambda)=S(p_1,...,p_n)+\lambda(\sum_{i=1}^np_i-1)\tag{1.25}
\] 极值条件为以下n+1个方程: \[
\begin{align}\frac{\partial L}{\partial
p_i}&=-(lnp_i+1)+\lambda=0\quad i=1,...,n\\
\frac{\partial L}{\partial \lambda}&=
\sum_{i=1}^np_i-1=0\end{align}\tag{1.26}
\] 则 \(p_1=\cdots
=p_n=\frac{1}{n},\lambda=1-ln{\,n}\).
可见无其他约束条件下,均匀分布使信息熵最大化。
正则系综(Canonical Ensemble)
There is, essentially, only one problem in statistical thermodynamics, the distribution of a given amount of energy E over identical systems. Or perhaps better, to determine the distribution of an assembly of identical systems over the possible states in which the system can find itself given that the energy of the assembly is a constant E.
——Schrodinger
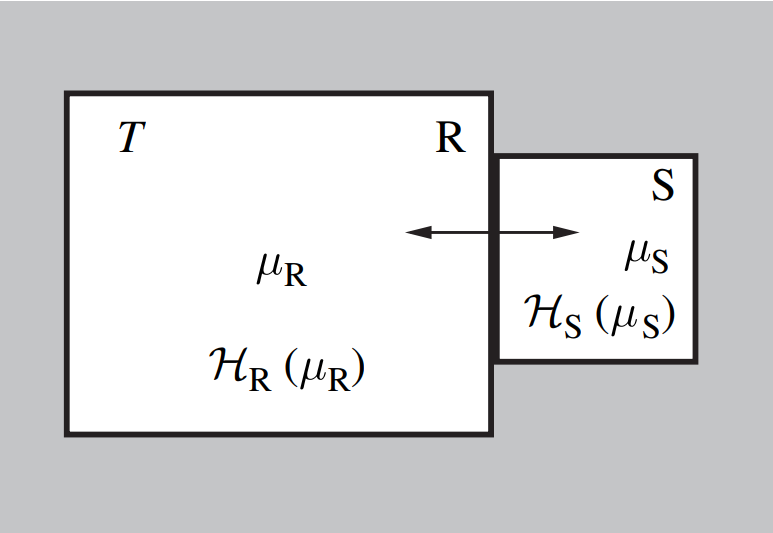
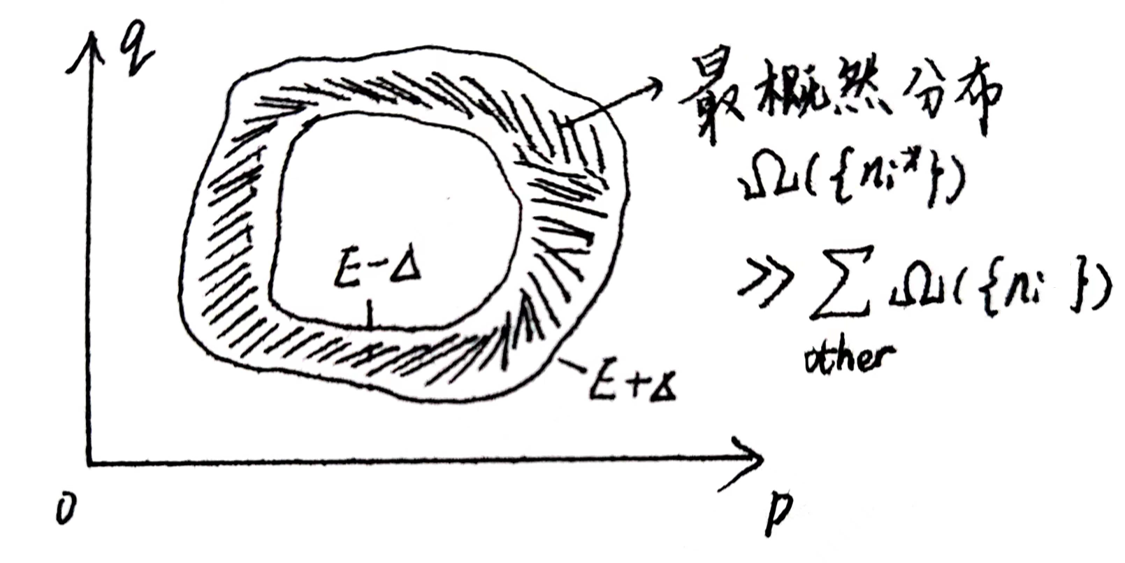
自然界和实验条件下,系统往往与环境有能量和物质交换,并非完全孤立。考虑实验上更容易制备和操控的宏观态\((N,V,T)\),其粒子数和体积固定,通过与环境的热平衡维持温度不变。系统达平衡时,包括内能所有热力学量不变。系综的平均能量不变,但每个瞬间系统的能量可任意取值。 考虑这样的系综:各个副本的体积和粒子数固定,相互之间可交换热量并达到热平衡,整个系综是孤立体系,总能不变(从而平均能量不变)。系综中的每个系统相当于浸没在无限大热浴中,这类似于推导系综概率分布的第一种方式。假设系统可能的微观态为\(\{\mu_i\}\), 系综的\(A\)个体系在各微观态上的一种分配方式构成组态(分布) \(C=\{n_i\}\),\(\{n_i\}\)是满足 \(\sum_{i} n_i=A\) 的所有可能整数集。宏观体系具有可分辨性,交换不同微观态上的系统产生新的组合,每种组态的组合数即为其统计权重\(W\{n_i\}=\frac{A!}{\prod_{i}n_i!}\),物理量的平均值为各组态对应值的加权平均: \[ <f>=\frac{\sum_{C=\{n_i\}}f\{n_i\}W\{n_i\}}{\sum_{C=\{n_i\}}W\{n_i\}}\tag{1.27} \] 当 \(A\to\infty\) ,\(W\{n_i\}\) 取得尖锐的极大值\(W\{n_i^*\}\)。最概然分布法的核心思想就是用占主导地位的\(\{n_i^*\}\)项取代式(1.27)的求和来计算系综平均。同时Boltzmann熵也用最概然分布的组合数计算,显然最终的公式与信息熵如出一致。相较于传统的繁琐方式,信息熵提供了等价而简洁的推导。
假设系综的微观态集合为 \(M=\{\mu_i\}\), 微观态的能量为\(E=\{\cal E_i\}\),对应的概率分布为\(\mathbf p=\{p_i\}\),在归一化条件和平均能量等于内能的约束下求最优分布: \[ \begin{align}max \quad S_I(\{p_i\})&=-\sum_{i}p_ilnp_i\\ s.t. \quad \sum_{i}p_i-1&=0\\ \quad \sum_{i}p_i{\cal E_i}-U&=0 \end{align}\tag{1.28} \] Lagrange函数: \[ L(p_i, \lambda)=S_I(p_i)+\alpha(\sum_{i}p_i-1)\tag{1.29}-\beta(\sum_{i}p_i{\cal E_i}-U) \] 极值条件: \[ \begin{align}\frac{\partial L}{\partial p_i}&=-(lnp_i+1)+\alpha-\beta {\cal E_i} =0\quad \\ \frac{\partial L}{\partial \alpha}&= \sum_{i}p_i-1=0\\ \frac{\partial L}{\partial \beta}&= -\sum_{i}p_i{\cal E_i}+U=0\end{align}\tag{1.30} \] 可得 \[ p_i=exp(\alpha-1)exp(-\beta {\cal E_i}) \tag{1.31} \] 从归一化条件得: \[ p_i=\frac{exp(-\beta {\cal E_i})}{Z(\beta)} \tag{1.32} \] 正则配分函数定义为 \(Z(\beta)=\sum_i exp(-\beta {\cal E_i})\),式中对所有可能的微观态求和。对经典系统: \(Z(\beta)=\frac{1}{h^{3N}N!}\int e^{-\beta \hat{\cal H}(\mathbf p,\mathbf q)} \,d\Gamma\). 热力学熵 \[ S=k_BS_I=k_B\beta U+k_BlnZ(\beta)\tag{1.33} \] 当N、V固定时,\(S\) 只是 \(\beta\) 和 \(U\) 的函数,这两个变量相互关联 :\(U=\sum_ip_i(\beta){\cal E_i}\)。根据温度的热力学定义: \[ \Bigl (\frac{\partial S}{\partial U}\Bigl )_{N,V}= \Bigl (\frac{\partial S}{\partial U}\Bigl )_{\beta,N,V}+\Bigl (\frac{\partial S}{\partial \beta}\Bigl )_{U,N,V}\Bigl (\frac{\partial \beta}{\partial U}\Bigl )_{N,V}=k_B\beta=\frac{1}{T}\tag{1.34} \] 因而\(\beta = 1/k_BT\),由此熵的定义桥接了统计力学和热力学。若已知正则配分函数,结合热力学基本关系可推导出所有的热力学量。其中Helmholz自由能与配分函数直接关联,是正则系综的特性函数: \[ F=-k_BT\,ln{Z(N,V,T)}\tag{1.35} \]
等温等压系综(Isothermal-isobaric Ensemble)
 \((N,P,T)\)
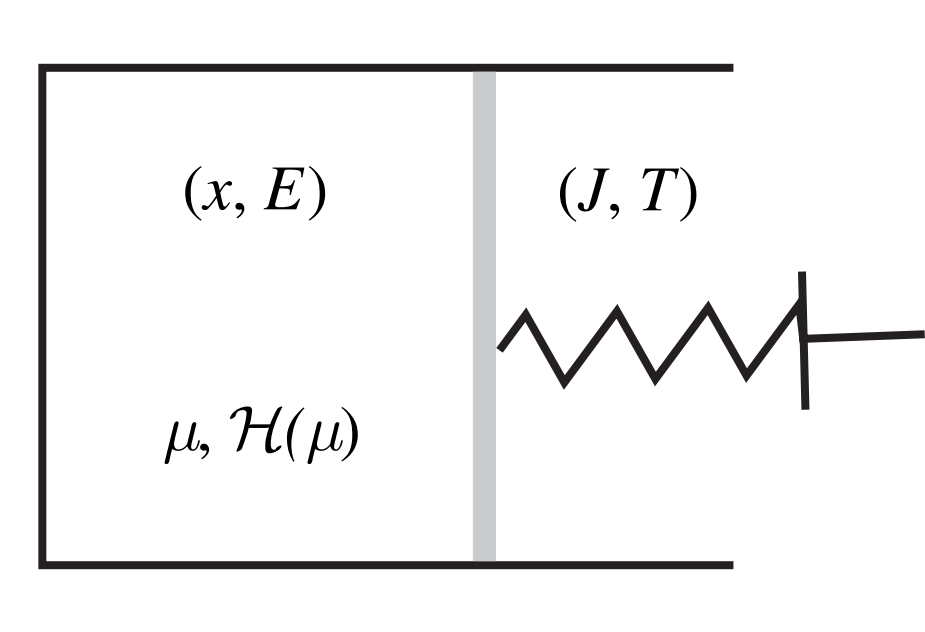
系综几乎是分子动力学模拟中最常用的系综,这源于自然界中等温等压环境的普遍性以及\((N,P,T)\)
系综与Gibbs自由能的直接关联。系统与环境交换热量和功达到平衡,保持温度T和压强P(广义力\(J\))稳定,能量E与体积V(广义位移x)在平衡值附近波动。相应的优化问题增加了约束条件:\(\sum_{i}p_i{\cal
V_i}-V=0\)。求解可得概率分布: \[
p_i=\frac{exp(-\frac{ {\cal E_i}+P{\cal V_i}}{k_BT})}{Z(N,P,T)}
\tag{1.36}
\] 配分函数 \[
\begin{align}Z(N,P,T)&=\sum_i exp(-\frac{ {\cal E_i}+P{\cal
V_i}}{k_BT})\\
\qquad \qquad \qquad \qquad \qquad &=\int_0^\infty
exp(-\frac{P{}V}{k_BT})\,Z(N,V,T)\,dV \end{align} \tag{1.37}
\] 等温等压系综的特性函数是Gibbs自由能: \[
G=-k_BT\,ln\,Z(N,P,T)\tag{1.38}
\] ### 巨正则系综(Grand Canonical Ensemble)
\((N,P,T)\)
系综几乎是分子动力学模拟中最常用的系综,这源于自然界中等温等压环境的普遍性以及\((N,P,T)\)
系综与Gibbs自由能的直接关联。系统与环境交换热量和功达到平衡,保持温度T和压强P(广义力\(J\))稳定,能量E与体积V(广义位移x)在平衡值附近波动。相应的优化问题增加了约束条件:\(\sum_{i}p_i{\cal
V_i}-V=0\)。求解可得概率分布: \[
p_i=\frac{exp(-\frac{ {\cal E_i}+P{\cal V_i}}{k_BT})}{Z(N,P,T)}
\tag{1.36}
\] 配分函数 \[
\begin{align}Z(N,P,T)&=\sum_i exp(-\frac{ {\cal E_i}+P{\cal
V_i}}{k_BT})\\
\qquad \qquad \qquad \qquad \qquad &=\int_0^\infty
exp(-\frac{P{}V}{k_BT})\,Z(N,V,T)\,dV \end{align} \tag{1.37}
\] 等温等压系综的特性函数是Gibbs自由能: \[
G=-k_BT\,ln\,Z(N,P,T)\tag{1.38}
\] ### 巨正则系综(Grand Canonical Ensemble)
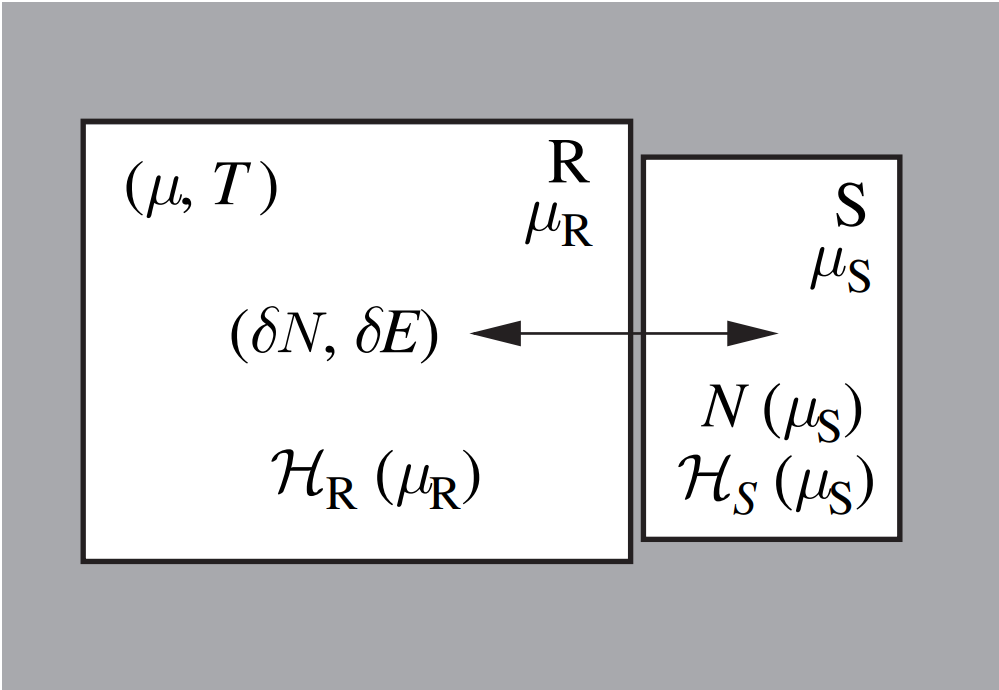 巨正则系综的系统与环境交换热量和粒子,宏观态由 \((\mu,V,T)\)
参量确定。在3个约束条件下求取最概然分布: \[
\begin{align}\quad \sum_{i}p_i-1&=0\\
\sum_{i}p_i{\cal E_i}-U&=0 \\
\sum_{i}p_i{\cal
N_i}-N&=0 \end{align}\tag{1.39}
\] 从而 \[
p(\mu_i)=\frac{exp(-\frac{ {\cal E_i}-\mu{\cal N_i}}{k_BT})}{Q(\mu,V,T)}
\tag{1.36}
\] 巨正则配分函数可用 N 粒子正则配分函数表达: \[
\begin{align}Q(\mu,V,T)&=\sum_{i}exp(-\frac{ {\cal E_i}-\mu{\cal
N_i}}{k_BT})\\
\quad \,\,\,\quad\qquad &=\sum_{N=0}^\infty e^{\mu
N/k_BT}\,Z(N,V,T)\tag{1.37}\end{align}
\] 定义 \(f=e^{\mu /k_BT}\)
为逸度。系统具有N个粒子的无条件概率为: \[
p(N)=\frac{e^{\mu N/k_BT}\,Z(N,V,T)}{Q(\mu,V,T)}\tag{1.38}
\] 巨正则系统的特性函数为巨势(grand potential): \[
\quad\Phi_G=-k_BT\,ln\,Q(\mu,V,T)=U-TS-\mu N=-PV\tag{1.39}
\] ## 涨落与系综等价性 正则系综能量的相对方均根涨落为 \[
\frac{\sqrt{\sigma_E^2}}{U}=\frac{\sqrt{<({\cal
E}-U)^2>}}{U}=k_B^{-1/2}T\frac{C_v^{1/2}}{U} \sim N^{-1/2} \tag{1.40}
\] 有限温度下当 \(N\to \infty\)
时,能量涨落趋于零。 而巨正则系综的粒子数涨落为(证明较复杂,利用\(\bigl (\frac{\partial \mu}{\partial
\overline{N}}\bigl)_{V,T}=-\frac{V^2}{\overline{N}^2}\big(\frac{\partial
p}{\partial V}\big)_{N,T}\)的关系): \[
\frac{\sqrt{\sigma_N^2}}{\overline{N}}=\frac{k_BT}{\overline{N}}\Bigl
(\frac{\partial \overline{N}}{\partial \mu}\Bigl
)_{V,T}=(k_BT\kappa_T/V)^{1/2}\sim N^{-1/2} \tag{1.41}
\] 其中等温压缩率 \(\kappa_T\)
是强度性质,对均相体系一般具有与N无关的有限值,因而上式成立。而对于临界点附近或相变区,\(\kappa_T\) 无穷大,以致粒子数涨落显著。
巨正则系综能量的方差为 \[
\sigma_E^2=−(\frac{∂U}{∂\beta})_{z,V}=k_BT^2C_V+k_BT\Bigl(\frac{∂U}{∂V}\Bigl)_{T,V}\Bigl(\frac{∂U}{∂μ}\Bigl)_{T,V}=\sigma_{E^2}(正则)+\Bigl\{\Bigl(\frac{∂U}{∂N}\Bigl)_{T,V}\Bigl
\}^2\sigma_N^2\tag{1.42}
\]
说明在巨正则系综中系统的能量的方均涨落等于在正则系综能量的方均涨落加上由于粒子数涨落所产生的贡献。一般情况下宏观相对能量涨落可以忽略,但在临界点和相变区,涨落的值受第二项影响而变得异常的大。
以上讨论表明,除了临界点和相变区,热力学极限下正则系综和巨正则系综的能量涨落和巨正则系综的粒子数涨落都可以忽略不计,相当于微正则系综\((N,V,E)\)。因而从正则系综和巨正则系综推导的热力学性质与微正则系综相同,热力学极限下各种系综等价。
巨正则系综的系统与环境交换热量和粒子,宏观态由 \((\mu,V,T)\)
参量确定。在3个约束条件下求取最概然分布: \[
\begin{align}\quad \sum_{i}p_i-1&=0\\
\sum_{i}p_i{\cal E_i}-U&=0 \\
\sum_{i}p_i{\cal
N_i}-N&=0 \end{align}\tag{1.39}
\] 从而 \[
p(\mu_i)=\frac{exp(-\frac{ {\cal E_i}-\mu{\cal N_i}}{k_BT})}{Q(\mu,V,T)}
\tag{1.36}
\] 巨正则配分函数可用 N 粒子正则配分函数表达: \[
\begin{align}Q(\mu,V,T)&=\sum_{i}exp(-\frac{ {\cal E_i}-\mu{\cal
N_i}}{k_BT})\\
\quad \,\,\,\quad\qquad &=\sum_{N=0}^\infty e^{\mu
N/k_BT}\,Z(N,V,T)\tag{1.37}\end{align}
\] 定义 \(f=e^{\mu /k_BT}\)
为逸度。系统具有N个粒子的无条件概率为: \[
p(N)=\frac{e^{\mu N/k_BT}\,Z(N,V,T)}{Q(\mu,V,T)}\tag{1.38}
\] 巨正则系统的特性函数为巨势(grand potential): \[
\quad\Phi_G=-k_BT\,ln\,Q(\mu,V,T)=U-TS-\mu N=-PV\tag{1.39}
\] ## 涨落与系综等价性 正则系综能量的相对方均根涨落为 \[
\frac{\sqrt{\sigma_E^2}}{U}=\frac{\sqrt{<({\cal
E}-U)^2>}}{U}=k_B^{-1/2}T\frac{C_v^{1/2}}{U} \sim N^{-1/2} \tag{1.40}
\] 有限温度下当 \(N\to \infty\)
时,能量涨落趋于零。 而巨正则系综的粒子数涨落为(证明较复杂,利用\(\bigl (\frac{\partial \mu}{\partial
\overline{N}}\bigl)_{V,T}=-\frac{V^2}{\overline{N}^2}\big(\frac{\partial
p}{\partial V}\big)_{N,T}\)的关系): \[
\frac{\sqrt{\sigma_N^2}}{\overline{N}}=\frac{k_BT}{\overline{N}}\Bigl
(\frac{\partial \overline{N}}{\partial \mu}\Bigl
)_{V,T}=(k_BT\kappa_T/V)^{1/2}\sim N^{-1/2} \tag{1.41}
\] 其中等温压缩率 \(\kappa_T\)
是强度性质,对均相体系一般具有与N无关的有限值,因而上式成立。而对于临界点附近或相变区,\(\kappa_T\) 无穷大,以致粒子数涨落显著。
巨正则系综能量的方差为 \[
\sigma_E^2=−(\frac{∂U}{∂\beta})_{z,V}=k_BT^2C_V+k_BT\Bigl(\frac{∂U}{∂V}\Bigl)_{T,V}\Bigl(\frac{∂U}{∂μ}\Bigl)_{T,V}=\sigma_{E^2}(正则)+\Bigl\{\Bigl(\frac{∂U}{∂N}\Bigl)_{T,V}\Bigl
\}^2\sigma_N^2\tag{1.42}
\]
说明在巨正则系综中系统的能量的方均涨落等于在正则系综能量的方均涨落加上由于粒子数涨落所产生的贡献。一般情况下宏观相对能量涨落可以忽略,但在临界点和相变区,涨落的值受第二项影响而变得异常的大。
以上讨论表明,除了临界点和相变区,热力学极限下正则系综和巨正则系综的能量涨落和巨正则系综的粒子数涨落都可以忽略不计,相当于微正则系综\((N,V,E)\)。因而从正则系综和巨正则系综推导的热力学性质与微正则系综相同,热力学极限下各种系综等价。
系综理论小结
宏观系统的状态由系统在各个微观态上确定的概率分布描述
稳态是概率分布不随时间变化
局域平衡态是稳态,且微观态(相点)之间的没有净的概率流(满足精细平衡原理)的概率分布。局域平衡态使得特性函数取极值。如微正则局域平衡态使得 \(S[\rho]\) 取极大值。
全局平衡态是最概然分布,使得特性函数取得全局最大/最小值的分布,如正则系综是使得\(A[\rho]\)取全局极小值的分布\(\rho_0\)。
通常我们讨论的平衡态都是局域平衡态,尤其是对复杂体系。平衡态是相对于一定时间定义的。例如重力场中的静置的玻璃,在几年之内其宏观性质都不会变化,但几十年甚至几万年后重力作用会使得它发生形变,在大的时间尺度上,原来的玻璃并没有处于全局平衡态。
但在通常的实验测量的时间尺度上,讨论全局平衡态没有太多意义。宏观体系的相空间几乎不能在通常的时间尺度、通常的条件下遍历,系统本身应该只局限于部分相空间。
只需要各态遍历、等概率公设、熵的统计定义三个假设,以及热力学量的定义和基本关系式,就可以推出不同条件下的平衡概率分布和用配分函数表达的热力学量。
量子系综理论的密度矩阵形式
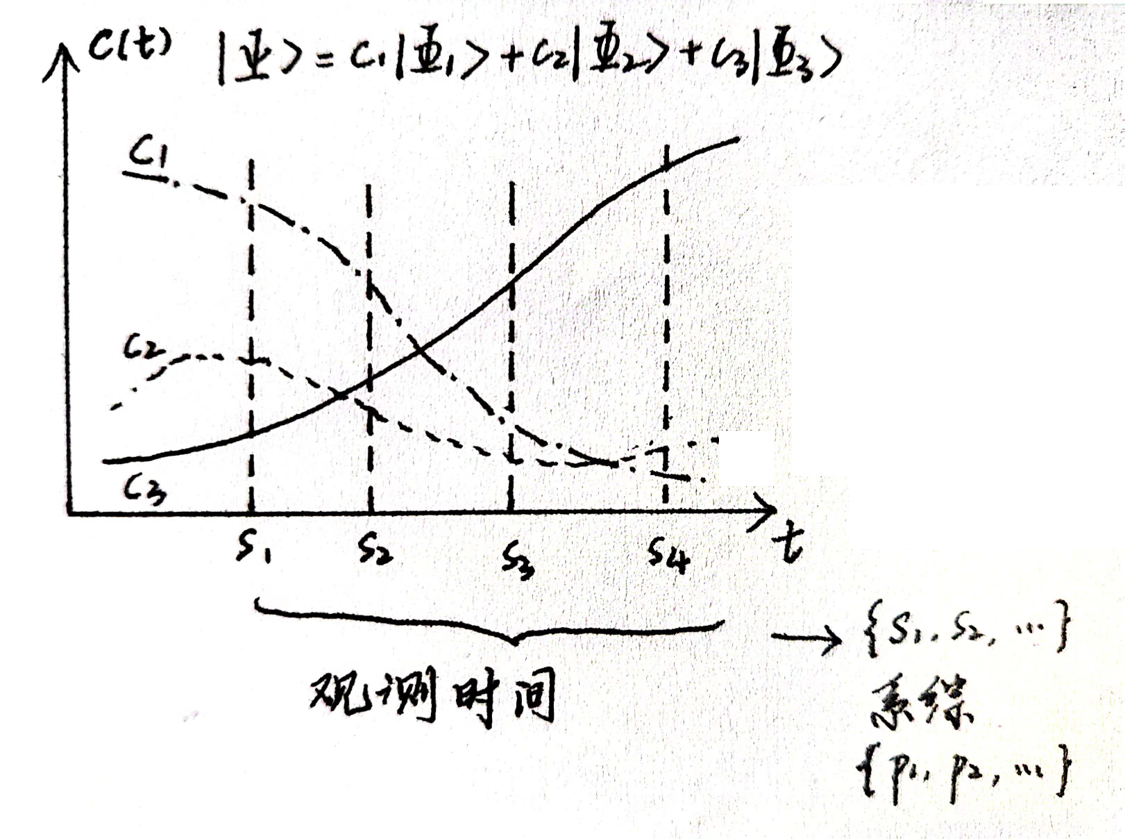 量子力学中,系统可能的微观态具有离散的取值(本征态),真实的状态为这些本征态的线性叠加。将配分函数中对可能微观态的求和写成对本征态求和,即可描述纯态的量子体系。但纯态的描述只适合孤立体系,对于与环境耦合的量子体系,微观态和宏观态的定义不同。
量子力学中,系统可能的微观态具有离散的取值(本征态),真实的状态为这些本征态的线性叠加。将配分函数中对可能微观态的求和写成对本征态求和,即可描述纯态的量子体系。但纯态的描述只适合孤立体系,对于与环境耦合的量子体系,微观态和宏观态的定义不同。
量子力学具有与不确定性关联的内在概率性,这导致量子统计中的两次求平均。考虑一个随时间演化的量子系统,在一段时间内观测系统,其宏观态表现为不同时刻的态矢\(\{s_1,s_2,...,s_n\}\)形成的混合态,物理量观测值就是这些微观态相应性质的时间平均,随时间段的移动观测值可能变化,也可能达到稳定——平衡态。然而对某一时刻的系统观测物理量\(f\),得到的观测值并不是确定值,而是一套本征值\(\{f_1,f_2,...\}\)中的一个,每种本征值出现的可能性与态矢关于本征矢的展开系数 \(\bra{\Phi_i}\ket{\Psi }\) 有关。如果制备许多相同的\(\ket{\Psi(t_0)}\),对应于 t0 时刻的系统,对这些样本(平行重复实验)观测的平均值就是期望值\(\bra {\Psi}\hat f\ket\Psi\)。这两种平均可分别可比作一台粒子加速器不同时刻的结果与多台加速器上同一时刻结果的统计。这样宏观物理量就是首先求物理量关于每个时刻对应态矢的期望值,再对不同时刻期望值求移动平均值 的结果。然而我们并不想求解宏观系统的含时薛定谔方程,参考经典统计的做法,我们将宏观态与态矢的集合\(\{\ket {\Psi_\alpha}\}\),以及相应的概率分布\(\{p_\alpha\}\)对应,这样这种时间移动平均就转换为对系综的统计平均。 现在让我们推导量子系综理论的表现形式。量子系统的微观态可由无限维Hilbert空间中的单位矢$$完全确定,即将态矢用正交归一的完备基集展开: \[ \ket \Psi =\sum_n \bra{n}\ket{\Psi}\ket{n} \tag{1.43} \] 归一化条件: \[ \bra {\Psi}\ket{\Psi}=\sum_n\bra{\Psi}\ket{n}\bra{n}\ket{\Psi}=1\tag{1.44} \] 物理量 \(O\) 的期望值为: \[ \left<\hat O\right> =\bra {\Psi}\hat O\ket{\Psi}=\sum_{n,m}\bra{\Psi}\ket{m}\bra{m}\hat O\ket{n}\bra{n}\ket{\Psi} \tag{1.45} \] \(O_{mn}=\bra{m}{\hat O}\ket{n}\) 为算符 \(\hat O\) 在正交基\(\{|n \ket\}\)下表示矩阵的矩阵元。矩阵 \(\bf O\) 是Hermitian矩阵。 考虑到系综的统计平均: \[ \overline{\left<\hat O\right>}=\sum_\alpha p_\alpha\bra {\Psi_\alpha}\hat O\ket{\Psi_\alpha}=\sum_{m,n}\sum_\alpha p_\alpha \bra{\Psi_\alpha}\ket{m}\bra{m}\hat O\ket{n}\bra{n}\ket{\Psi_\alpha} =\sum_{m,n}\bra{n}{\hat \rho}\ket{m} O_{mn}=tr(\bf \rho O)\tag{1.46} \] 这里我们定义了密度算符: \[ \hat \rho(t)=\sum_\alpha p_\alpha\ket{\Psi_\alpha}\bra{\Psi_\alpha} \tag{1.47} \] 当且仅当系综只由一个态矢描述,\(\hat \rho(t)=\ket{\Psi}\bra{\Psi }\) 即 \(\bf \rho^2=\rho\) 时,称之为纯态(pure state)系综。 密度矩阵(density matrix)具有以下性质:(1)归一化(Normalization) \(tr(\rho)=\sum_\alpha p_\alpha=1\) (2)厄米性(Hermiticity) (3)正定性。 由式(1.46),只需知道密度矩阵 \(\rho\) 和 算符 \(\hat O\) 的矩阵表示,就可以计算物理量O的系综平均。这表明系统的宏观态可由密度矩阵完全确定。类似经典统计中将系统的宏观态映射到相空间中的密度分布,量子统计将宏观态映射到Hilbert空间中的密度矩阵。 现在让我们考虑密度矩阵随时间的演化。我们知道态矢的演化遵循含时薛定谔方程: \[ i\hbar \frac{\partial}{\partial t}\ket{\Psi(t)}=\hat {\cal H}\ket{\Psi(t)} \tag{1.48} \] 自然地,我们采用能量本征态展开态矢,则有: \[ i\hbar \frac{\partial}{\partial t}\bra{n}\ket{\Psi}=\cal E_n\bra{ n}\ket{\Psi} \tag{1.49} \] 则 \[ i\hbar \frac{\partial}{\partial t}\bra{n}{\hat \rho(t)}\ket{m}=\sum_\alpha p_\alpha[(\cal E_n-\cal E_m)\bra{n}\ket{\Psi_\alpha}\bra{\Psi_\alpha}\ket{m}] =\bra{n}{\hat{\cal H}\rho-\rho\hat {\cal H} }\ket{m}\tag{1.50} \] 这是一个张量不变的等式,即与基集的选择无关。这就是量子Liouville方程: \[ i\hbar \frac{\partial}{\partial t}\hat \rho=[\hat {\cal H},\hat \rho]\tag{1.51} \] 类似于经典统计,如果\(\hat \rho=\hat \rho(\hat{\cal H})\),则 \(\partial {\hat \rho} /\partial t=0\) (可证明量子力学算符的对易子等于经典的Poisson括号乘以 \(i\hbar\) ,因而 \(\hat{\cal H}\) 与 \(\hat \rho\) 对易)。如同基于相空间的经典统计,基于密度矩阵的形式,量子统计也建立了严格的框架。在密度矩阵的形式中重新表述系综理论: - 微正则系综密度算子为
\[ \hat \rho(E)=\frac{\delta(\hat {\cal H}-E)}{\Omega(E)}\tag{1.52} \] 其矩阵元 \[ \bra{n}{\hat \rho}\ket{m}=\begin{cases}1/\Omega \quad if\,{\cal E_n}=E,\,\,and\,\,\, m=n\\ 0 \quad if \,{\cal E_n}\neq E,\,\, or\,\,\, m\neq n\end{cases}\tag{1.53} \] 其中\(\Omega(E)\)就是能量为E的本征态数目。需提及由于 \([\hat {\cal H},\hat \rho]=0\),在能量本征态基集下密度矩阵对角化,因而 \(m\neq n\) 的矩阵元为0。 值得一提的是纯态系综 \(\Omega=1\),对应于热力学第三定律所言熵为0的情况,而混合态系综的熵大于0。 等概率假设导致了式(1.53)中对角元相同,为了保证在其他表象中该条件仍成立,还需无规相位假设。
==为什么需要密度矩阵?是因为波函数表达的是一系列相互纠缠的态,而与环境接触达到热平衡的体相,各个态之间显然不是完全关联,其相位随机取向,密度矩阵表达的是就是这样微观态随机出现的宏观态。(这部分还有待细看)==
- 正则系综
\[ \hat \rho(\beta)=\frac{exp(-\beta\hat {\cal H})}{Z(\beta)}\tag{1.53} \] 算子根据麦克劳林展开定义:\(e^{-\beta \hat{\cal H}}= 1-\beta\hat {\cal H}+\frac{1}{2}\beta^2 \hat {\cal H}^2+\cdots\) 。显然其作用于能量本征态上得到 \(e^{-\beta \cal E}\) 。 根据密度矩阵的归一化条件,配分函数: \[ Z(\beta)=tr(e^{-\beta \hat{\cal H}})=\sum_\mu e^{-\beta \cal E(\mu)}\tag{1.54} \] 得到与之前假设离散的微观态相同的结果。因而我们可以通过在任意正交基下计算\(e^{-\beta \hat{\cal H}}\)的矩阵元并求矩阵的迹来得到配分函数,也可以对角化Hamiltonian矩阵,得到能量本征值(及简并度)从而计算配分函数。 - 巨正则系综
\[ \rho(\beta,\mu)=\frac{e^{-\beta \hat {\cal H}+\beta \mu\hat N}}{Q} \tag{1.55} \] \[ Q(\beta,\mu)=tr(e^{-\beta \hat {\cal H}+\beta \mu\hat N})=\sum_{N=0}^\infty e^{\beta \mu N}Z(N,\beta)\tag{1.56} \] 经典统计中,密度函数 \(\rho(\bf p,q)\) 表示相空间某一点的概率密度。而在量子统计中,密度矩阵的对角元 \(\rho_{nn}\) 表示基函数\(\ket{n}\)权重的统计平均 \(\sum_np_\alpha \bra{n} \ket{\Psi_\alpha }\bra{\Psi_\alpha}\ket{n}\). 如果我们将\(\ket{\Psi_\alpha}\)设为本征态(这是相当自然的事情),并在能量表象下写出密度矩阵,则其对角元 \(\rho_n = p_n\) 就是本征态\(\ket{n}\)的出现概率(平衡态下密度矩阵与Hamiltonian具有共同本征态,其本征值就是概率)。量子与经典统计的相似性显而异见。
##各种系综的比较以及热力学量计算
这里比较了各种系综的概率分布函数、归一化系数的表达式。 
理想气体:从量子统计到经典统计
由于粒子不可分辨性对波函数对称性施加的约束,确定合法的能量本征态并非易事。即使对理想气体,我们能很容易对角化单粒子Hamiltonian,从单粒子能量本征值推断多粒子体系的允许能级,我们仍需费一些功夫筛选符合波函数交换对称性的多粒子态,确定态密度,从而才能计算配分函数。
首先我们讨论对波函数的一般要求。由于粒子的全同性,交换两个粒子的空间-自旋坐标并不产生新的状态,概率密度保持不变:
\[
|\Psi(\vec q_1,\vec q_2)|^2=|\Psi(\vec q_2,\vec q_1)|^2\tag{1.57}
\] 这就要求对交换两个粒子坐标的操作,波函数不变或反号:\(\ket{\Psi(\vec q_1,\vec q_2)} = \ket{\Psi(\vec
q_2,\vec q_1)}\) or \(\ket{\Psi(\vec
q_1,\vec q_2)} = -\ket{\Psi(\vec q_2,\vec
q_1)}\)。更一般地,对交换粒子坐标产生新排列的置换操作\(\hat
P\),有对称和反对称的波函数,分别对应自然界中的玻色子(Bosons)和费米子(Fermions):
\[
\begin{align}Bosons:\quad \hat
P\ket{\Psi(1,...,N)}&=+P\ket{\Psi(1,...,N)}\\
Fermions:\quad \hat
P\ket{\Psi(1,...,N)}&=(-1)^PP\ket{\Psi(1,...,N)}\tag{1.58}\end{align}
\] 其中P是产生排列所需的置换次数。显然置换不使Hamiltonian改变。
现在考虑量子理想气体。假设我们已经对角化单粒子Hamiltonian \(\hat h\),得到单粒子本征态\(\{\ket{\psi}\}\)。现在我们构造N粒子态。显然乘积态(product
state) \(\ket{\psi_1,...,\psi_N}_\otimes=\ket{\psi_1(1)}\cdots\ket{\psi_N(N)}\)是Hamiltonian
\(\hat {\cal H}=\sum_{\alpha=1}^N \hat
h_\alpha\)
的本征态,但它不满足对任意置换操作保持不变或反号的要求。为此需用所有可能的
N! 个乘积态线性组合来构造N粒子态。
对费米子,反对称(anti-symmetric)的N粒子态为Slater行列式(虽然是Dirac发明):
\[
\ket{\Psi}=\frac{1}{\sqrt N!}\sum_P(-1)^P\hat
P\ket{\psi_1(1),...,\psi_N(1)}_\otimes=\frac{1}{\sqrt N!}
\begin{vmatrix}
\psi_1(1) &\psi_2(1) &\cdots &\psi_N(1)\\
\psi_1(2) &\psi_2(2) &\cdots &\psi_N(2)\\
\vdots & \vdots & & \vdots \\
\psi_1(N)& \psi_2(N) &\cdots &\psi_N(N)
\end{vmatrix} \tag{1.59}
\] 其要求组成乘积态的单粒子态不能有重复,否则行列式为0。
对玻色子则没有任何对单粒子态出现次数的限制。假设乘积态中每个占据态的出现次数为\(\{n_{i}\}\), 满足 \(\sum_{i=1}^{occ}n_i=N\).
如果有重复出现的单粒子态,则式(1.60)的求和中必有重复的乘积态项,化简后不重复的项数为
\(\frac{N!}{\prod_i^{occ}n_i!}\)。又由于单粒子态的正交归一,序列不同的乘积态之间矩阵元为0,只有序列相同的之间矩阵元为1,可得归一化系数
\(N_+=N!\prod_i^{occ}n_i\)。 \[
\ket{\Psi}=\frac{1}{\sqrt N_+}\sum_P\hat
P\ket{\psi_1(1),...,\psi_N(1)}_\otimes\tag{1.60}
\]
费米子和玻色子波函数对称性对单粒子态填充的限制不同,造就了它们不同的统计。对费米子,一个单粒子态上的占据数为0或1(Fermi-Dirac统计);对玻色子,占据数可取任意自然数
(Bose–Einstein统计)。
现在我们计算配分函数。由于粒子的全同性,N粒子态完全由一组占据数\(\{n_i\}\)(组态)确定,则: \[
Z_N(\beta)=tr(e^{-\beta \hat {\cal H}})=\sum_{s.t. \sum_i
n_i=N}exp(-\beta \sum_i\cal E_in_i)\tag{1.61}
\] 其中\(\cal
E_i\)是单粒子态的能量。
除了占据数之和等于N的约束1,占据数还受到粒子本身交换对称性的约束2。我们难以计算式(1.61)的约束求和。Kardar展示了在坐标表象下求正则配分函数的一系列复杂操作,然而在能量表象下我们可以绕过
\(Z_N\)。通过对所有可能的N值求和,将两次求和变为一次解除约束1的求和(这样占据数就可以相互独立变化,这是一个令人印象深刻的技巧):
\[
Q(\mu,\beta)=\sum_{N=0}^\infty e^{\beta \mu N}\,Z_N(\beta)
=\sum_{N=0}^\infty\sum_{\{n_i\}'}\prod_i e^{-\beta(\cal
E_i-\mu)n_i}=\sum_{\{n_i\}}\prod_i e^{-\beta(\cal E_i-\mu)n_i}=\prod_i
\sum_{n_i}e^{-\beta(\cal E_i-\mu)n_i} \tag{1.62}
\]
最后面的连乘是对所有的单粒子态进行,求和是对所有满足对称性要求的
ni 进行: \[
\begin{align}&For\,\, fermions,\,n_i=0\,\,or\,\,1: \\
&Q_-=\prod_i[1+exp(\beta \mu-\beta{\cal E_i})]\\
&For\,\, bosons,\,n_i=0,1,2,...:\\
&Q_+=\prod_i[1-exp(\beta\mu-\beta {\cal
E_i})]^{-1}\end{align}\tag{1.63}
\] N粒子态\(\ket{\{n_i\}
}\)的出现概率为: \[
p(\ket{\{n_i\} })=\frac{1}{Q}\prod_iexp(\beta\mu-\beta{\cal
E}_i)\tag{1.64}
\]
不打算在本文中列出详细的推导,只说结论。无论是从何种表示出发,我们都得出量子气体表现得如同相互作用气体,其virial状态方程为(其中g为自旋多重度2s+1,对fermions
\(\eta=-1\),对boson \(\eta=+1\)s;热波长\(\lambda=\frac{\hbar}{\sqrt{2\pi k_B
T}}\)):
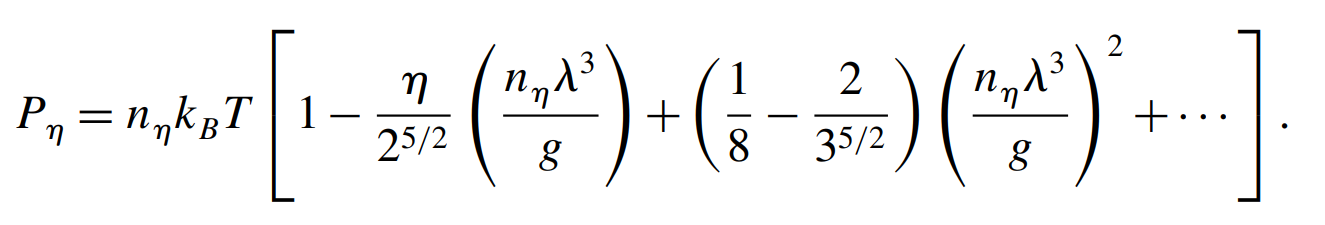 非简并情况的正则配分函数:
非简并情况的正则配分函数:
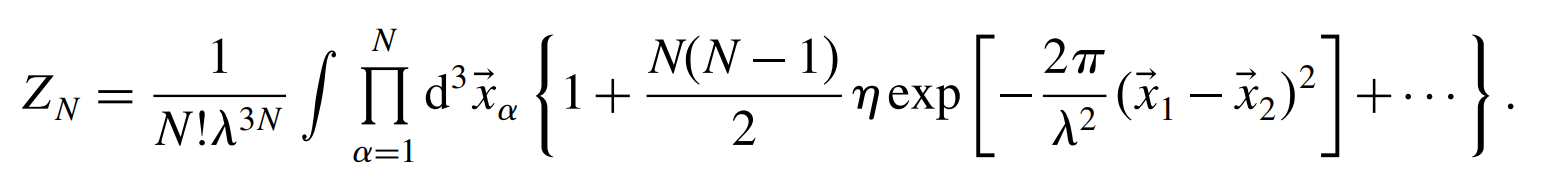 我们看到量子效应的大小由简并参数 \(\frac{n_\eta \lambda^3}{g}\)
衡量,在高温、低密度极限(热波长远小于粒子间距,波函数几乎不重叠),单粒子态充分可及,交换作用效应很小,状态方程和配分函数只保留第一项,与经典的结果相同。然而在低温高密度
,状态方程的二阶、三价等高阶项变得重要,使体系偏离理想气体。其情形就像粒子之间存在相互作用势:费米子相互排斥、玻色子相互吸引。这实际上是因为波函数对称性的约束使得粒子的空间分布不再相互独立,粒子间存在空间(可能还加上自旋)关联作用。配分函数的第二项即对应两个粒子的交换作用,导致状态方程中的二阶virial系数,高阶项则对应三体、四体等多体作用,可以用团簇展开技术求解这些项。
我们看到量子效应的大小由简并参数 \(\frac{n_\eta \lambda^3}{g}\)
衡量,在高温、低密度极限(热波长远小于粒子间距,波函数几乎不重叠),单粒子态充分可及,交换作用效应很小,状态方程和配分函数只保留第一项,与经典的结果相同。然而在低温高密度
,状态方程的二阶、三价等高阶项变得重要,使体系偏离理想气体。其情形就像粒子之间存在相互作用势:费米子相互排斥、玻色子相互吸引。这实际上是因为波函数对称性的约束使得粒子的空间分布不再相互独立,粒子间存在空间(可能还加上自旋)关联作用。配分函数的第二项即对应两个粒子的交换作用,导致状态方程中的二阶virial系数,高阶项则对应三体、四体等多体作用,可以用团簇展开技术求解这些项。
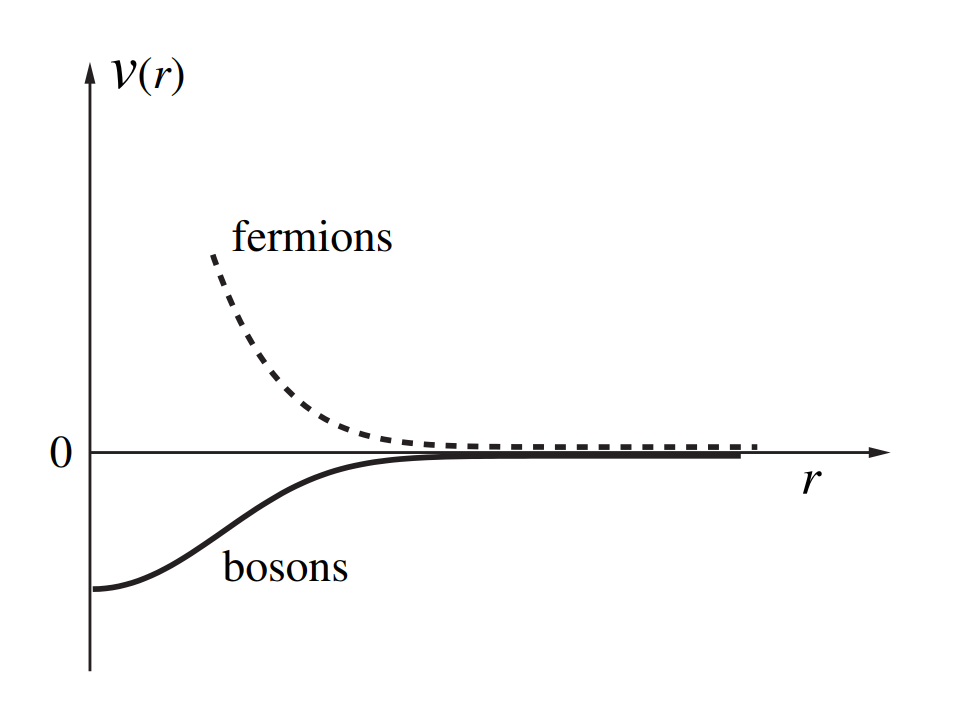 化学向的书在处理这部分内容常常采用最概然分布近似,只考虑粒子在能级上最可能的分布方式对微观状态数的贡献(微正则系综)。在热力学极限下,最概然分布形成尖锐的极大,其结果理与严格处理一致。
化学向的书在处理这部分内容常常采用最概然分布近似,只考虑粒子在能级上最可能的分布方式对微观状态数的贡献(微正则系综)。在热力学极限下,最概然分布形成尖锐的极大,其结果理与严格处理一致。
 至此,我们以较严谨的方式搭建了统计力学基础,并完成了量子到经典的过渡。我们看到,高温、低密度极限下,经典统计近似成立,对于质量较大的粒子,其相同温度下其热波长较小,量子效应相对不显著。这构成了我们今后遇到的大多数情况下,将原子核/原子当做经典粒子处理的前提。对于无相互作用体系(固体中的相互独立的声子和理想气体),我们可以用Maxwell-Boltzmann统计处理,即当做可分辨粒子计数,但用除以N!因子校正。对于相互作用的复杂体系,我们需要借助各种算法来进行构型采样(仍视原子为可分辨的粒子),获取能谱来计算配分函数(进行校正)。
补充:巨正则系综中无自旋气体的平均能量和粒子数
至此,我们以较严谨的方式搭建了统计力学基础,并完成了量子到经典的过渡。我们看到,高温、低密度极限下,经典统计近似成立,对于质量较大的粒子,其相同温度下其热波长较小,量子效应相对不显著。这构成了我们今后遇到的大多数情况下,将原子核/原子当做经典粒子处理的前提。对于无相互作用体系(固体中的相互独立的声子和理想气体),我们可以用Maxwell-Boltzmann统计处理,即当做可分辨粒子计数,但用除以N!因子校正。对于相互作用的复杂体系,我们需要借助各种算法来进行构型采样(仍视原子为可分辨的粒子),获取能谱来计算配分函数(进行校正)。
补充:巨正则系综中无自旋气体的平均能量和粒子数
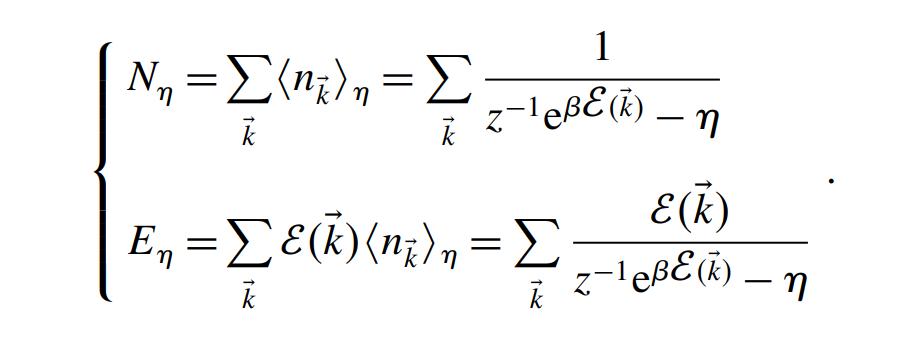
参考资料
- Kardar, M. (2007). Statistical Physics of Particles. Cambridge: Cambridge University Press.
- Stephen Blundell & Katherine M. Blundell. (2010). Concepts in Thermal Physics. Oxford: Oxford University Press.


